详解深度学习感知机原理( 二 ) 大家好

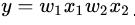文章插图
。这里的y是一个浮点数，我们可以在y上套一个sign函数。所谓的sign函数，即使根据阈值来进行分类。比如我们设置一个阈值
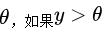文章插图
，如果
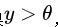文章插图
，那么
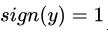文章插图
，否则的话
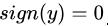文章插图
。
说起来又是神经元又是感知机什么的，但它的原理很简单，我们把公式写出来就是:
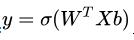文章插图
，这里的
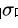文章插图
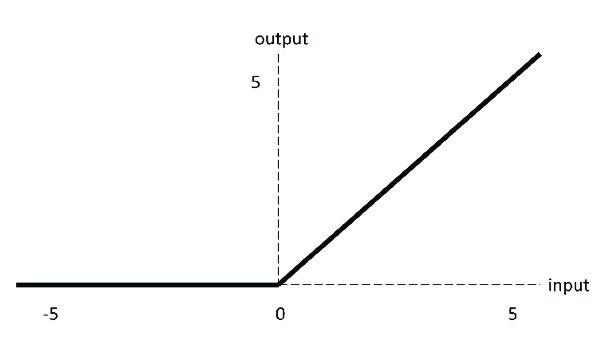
叫做激活函数(activate function) 。我们上面列举的例子当中的激活函数是sign函数，也就是根据阈值进行分类的函数。在神经网络当中常用的激活函数主要有三种，一种是我们之前就非常熟悉的sigmoid函数，一种是relu函数，另外一种是tanh函数。我们来分别看下他们的图像。
文章插图
relu函数的方程很简单：
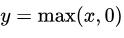文章插图
。但是它的效果非常好，也是神经网络当中最常用的激活函数之一。使用它的收敛速度要比sigmoid更快，原因也很简单，因为sigmoid函数图像两边非常非常光滑，导致我们求导得出的结果非常接近0 ，这样我们梯度下降的时候自然收敛速度就慢了。这一点我们之前在介绍sigmoid函数的时候曾经提到过。
文章插图
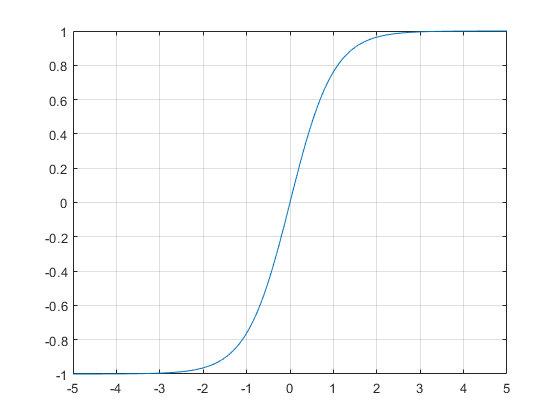
从图像上来看tanh函数和sigmoid函数非常相似，一点细微的差别是他们的值域不同， sigmoid函数的值域是0到1 ，而tanh是-1到1 。虽然看起来只是值域不同，但是区别还是挺大的，一方面是两者的敏感区间不同。 tanh的敏感区间相比来说更大，另外一点是， sigmoid输出的值都是正值，在一些场景当中可能会产生问题。
相信大家看出来了，感知机其实就是一个线性方程再套上一个激活函数。某种程度上来说逻辑回归模型也可以看成是一个感知机。有一个问题大家可能感到很疑惑，为什么线性方程后面需要加上一个激活函数呢？如果不加行不行？
答案是不行，原因也很简单，因为当我们把多个神经元组织在一起形成了一张网络之后。如果每一个神经元的计算都是这样纯线性的，那么整个神经网络其实也等价于一个线性的运算。这个是可以在数学上得到证明的，所以我们需要在感知机当中增加一点东西，让它的计算结果不是纯线性的。
感知机和逻辑电路最后我们来看一个实际一点的例子，最简单的例子当然是逻辑电路当中的与或门。与门、或门、非门其实都差不多，都是有两个输入和一个输出。
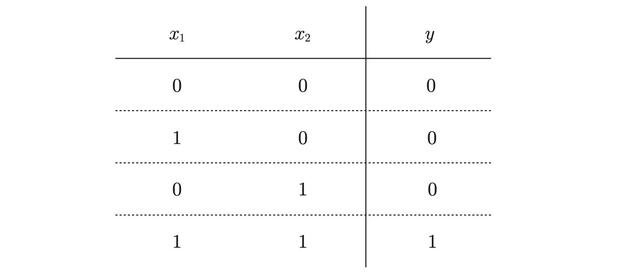
我们以与门为例：
文章插图
二进制的与操作我们都很熟悉了，只有两个数都为1才能得到1 。我们要写出这样一个感知机来也非常简单：