leetcode1614_go_括号的最大嵌套深度题目如果字符串满足一下条件之一

题目如果字符串满足一下条件之一，则可以称之为有效括号字符串（valid parentheses string ，可以简写为 VPS）：
字符串是一个空字符串 "" ，或者是一个不为 "(" 或 ")" 的单字符。
字符串可以写为 AB（A 与 B 字符串连接），其中 A 和 B 都是有效括号字符串。
字符串可以写为 (A) ，其中 A 是一个有效括号字符串。
类似地，可以定义任何有效括号字符串 S 的嵌套深度 depth(S)：
depth("") = 0
depth(A + B) = max(depth(A), depth(B)) ，其中 A 和 B 都是有效括号字符串
depth("(" + A + ")") = 1 + depth(A) ，其中 A 是一个有效括号字符串
例如：""、"()()"、"()(()())" 都是有效括号字符串（嵌套深度分别为 0、1、2），
而 ")(" 、"(()" 都不是有效括号字符串。
给你一个有效括号字符串 s ，返回该字符串的 s 嵌套深度。
示例 1：输入：s = "(1+(2*3)+((8)/4))+1" 输出：3
解释：数字 8 在嵌套的 3 层括号中。
示例 2：输入：s = "(1)+((2))+(((3)))" 输出：3
示例 3：输入：s = "1+(2*3)/(2-1)" 输出：1
示例 4：输入：s = "1" 输出：0
提示： 1 <= s.length <= 100
s 由数字 0-9 和字符 '+'、'-'、'*'、'/'、'('、')' 组成
题目数据保证括号表达式 s 是有效的括号表达式
解题思路分析1、遍历；时间复杂度O(n) ，空间复杂度O(1)
func maxDepth(s string) int { res := 0 count := 0 for i := 0; i < len(s); i++ {if s[i] == '(' {count++} else if s[i] == ')' {if count > res {res = count}count--} } return res}2、栈辅助；时间复杂度O(n) ，空间复杂度O(n)
文章插图
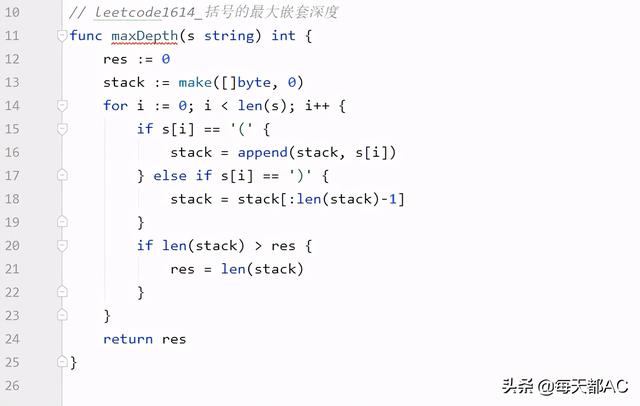
func maxDepth(s string) int { res := 0 stack := make([]byte, 0) for i := 0; i < len(s); i++ {if s[i] == '(' {stack = append(stack, s[i])} else if s[i] == ')' {stack = stack[:len(stack)-1]}if len(stack) > res {res = len(stack)} } return res}总结【leetcode1614_go_括号的最大嵌套深度】Easy题目，题目数据有效，直接左括号入栈，右括号出栈即可