有关自然语言处理的深度学习知识有哪些？( 五 ) .font_s.ios.pgcarticle

注意
代码清单5-3中的代码通过一个单层感知机解决了或问题。代码清单5-1代码中感知机学到的0和1组成的表格是二元逻辑或的输出结果。异或问题稍微改变了一下该数据表，以此来教感知机如何模拟一个独占的逻辑或门。如果改变一下最后一个示例的正确结果，将1（真）改为0（假），从而将其转换为逻辑异或，这个问题就会变得困难许多。在不向神经网络添加额外神经元的情况下，每类（0或1）样本将是非线性可分的。在二维特征向量空间中，这些类彼此呈对角线分布（类似于图5-5），所以无法通过画一条直线来区分出数据样本1（逻辑真）和0（逻辑假）。
尽管神经网络可以解决复杂的非线性问题，但是那时计算成本太高，用两个感知机和一堆花哨的反向传播数学算法来解决异或问题被认为是对宝贵计算资源的极大浪费，因为这个问题只需要用一个逻辑门或一行代码就能解决。事实证明，它们不适合被广泛使用，所以只能再次回到学术界和超级计算机实验的角落。由此开启了第二次“人工智能寒冬” ，这种情况从1990年持续到2010年左右[9] 。后来，随着计算能力、反向传播算法和原始数据（例如猫和狗的标注图像[10]）的发展，昂贵的计算算法和有限的数据集都不再是障碍。第三次神经网络时代开始了。
下面我们来看看他们发现了什么。
5．第二次人工智能寒冬的出现和大多数伟大的思想一样，好的思想最终都会浮出水面。人们发现只要对感知机背后的基本思想进行扩展，就可以克服之前的那些限制。将多个感知机集合到一起，并将数据输入一个（或多个）感知机中，并且以这些感知机的输出作为输入，传递到更多的感知机，最后将输出与期望值进行比较，这个系统（神经网络）便可以学习更复杂的模式，克服了类的线性不可分的挑战，如异或问题。其中的关键是：如何更新前面各层中的权重？
接下来我们暂停一下，将这个过程的一个重要部分形式化。到目前为止，我们已经讨论了误差和感知机的预测结果与真实结果的偏离程度。测量这个误差是由代价函数或损失函数来完成的。正如我们看到的，代价函数量化了对于输入“问题”（x）网络应该输出的正确答案与实际输出值（y）之间的差距。损失函数则表示网络输出错误答案的次数以及错误总量。公式5-2是代价函数的一个例子，表示真实值与模型预测值之间的误差：
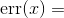文章插图
公式5-2　真实值与预测值之间的误差
训练感知机或者神经网络的目标是最小化所有输入样本数据的代价函数。
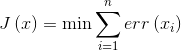文章插图
公式5-3　希望最小化的代价函数
接下来大家会看到还有一些其他种类的代价函数，如均方误差，这些通常已经在神经网络框架中定义好了，大家无须自己去决定哪些是最好的代价函数。需要牢记的是，最终目标是将数据集上的代价函数最小化，这样此处给出的其他概念才有意义。
6．反向传播算法辛顿（Hinton）和他的同事提出一种用多层感知机同时处理一个目标的方法。这个方法可以解决线性不可分问题。通过该方法，他们可以像拟合线性函数那样去拟合非线性函数。
【有关自然语言处理的深度学习知识有哪些？】但是如何更新这些不同感知机的权重呢？造成误差的原因是什么？假设两个感知机彼此相邻，并接收相同的输入，无论怎样处理输出（连接、求和、相乘），当我们试图将误差传播回到初始权重的时候，它们（输出）都将是输入的函数（两边是相同的），所以它们每一步的更新量都是一样的，感知机不会有不同的结果。这里的多个感知机将是冗余的。它们的权重一样，神经网络也不会学到更多东西。