目标检测算法中规则矩形和不规则矩形IOU的Python实现交并比（Intersection-over-Union

文章插图
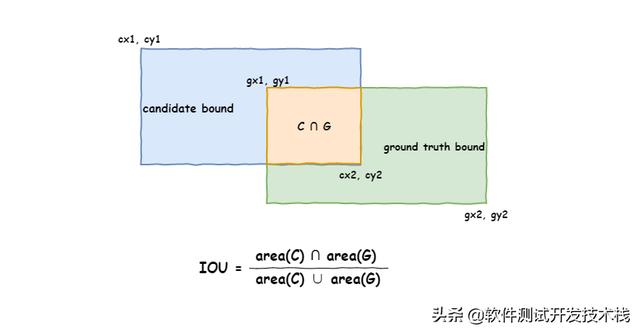
交并比（Intersection-over-Union ， IoU），目标检测中使用的一个概念，我们在进行目标检测算法测试时，重要的指标，是产生的预测框（candidate bound）与标记框（ground truth bound）的交叠率，即它们的交集与并集的比值。最理想情况是完全重叠，即比值为1 。
通常，我们所说的目标检测检测的框是规则的矩形框，计算IOU也非常简单，一般两种方法：

两个矩形的宽之和减去组合后的矩形的宽就是重叠矩形的宽，同比重叠矩形的高。

右下角的最小值减去左上角的最大值就是重叠矩形的宽，同比高。

上述规则四边形（矩形）IOU计算方式一的 Python实现

def calculate_regular_iou(rec1, rec2):"""computing IoU:param rec1: (y0, x0, y1, x1), which reflects(top, left, bottom, right):param rec2: (y0, x0, y1, x1):return: scala value of IoU"""S_rec1 = (rec1[2] - rec1[0]) * (rec1[3] - rec1[1])S_rec2 = (rec2[2] - rec2[0]) * (rec2[3] - rec2[1])?sum_area = S_rec1 + S_rec2?left_line = max(rec1[1], rec2[1])right_line = min(rec1[3], rec2[3])top_line = max(rec1[0], rec2[0])bottom_line = min(rec1[2], rec2[2])?if left_line >= right_line or top_line >= bottom_line:return 0else:intersect = (right_line - left_line) * (bottom_line - top_line)return (intersect / (sum_area - intersect)) * 1.0if __name__ == '__main__':# (top, left, bottom, right)rect1 = [551, 26, 657, 45]rect2 = [552, 27, 672, 46]iou = calculate_regular_iou(rect1, rect2)

上述规则四边形（矩形）IOU计算方式二的 Python 实现

def compute_regular_iou_other(rec1, rec2):"""computing IoU:param rec1: (y0, x0, y1, x1), which reflects(top, left, bottom, right):param rec2: (y0, x0, y1, x1):return: scala value of IoU"""areas1 = (rec1[3] - rec1[1]) * (rec1[2] - rec1[0])areas2 = (rec2[3] - rec2[1]) * (rec2[2] - rec2[0])?left = max(rec1[1],rec2[1])?right = min(rec1[3],rec2[3])?top = max(rec1[0], rec2[0])?bottom = min(rec1[2], rec2[2])?w = max(0, right - left)h = max(0, bottom - top)?return w*h / (areas2 + areas1 - w*h)?if __name__ == '__main__':# (top, left, bottom, right)rect1 = [551, 26, 657, 45]rect2 = [552, 27, 672, 46]iou = compute_regular_iou_other(rect1, rect2)

但是，对于不规则四边形就不能通过上述这两种方式来计算，这里可以使用Python的 Shapely 库实现， Python 实现如下：

import numpy as npimport shapelyfrom shapely.errors import TopologicalErrorfrom shapely.geometry import Polygon,MultiPoint?def to_polygon(quadrilateral):"""?:param quadrilateral: 四边形四个点坐标的一维数组表示 ， [x,y,x,y....]:return: 四边形二维数组, Polygon四边形对象"""# 四边形二维数组表示quadrilateral_array = np.array(quadrilateral).reshape(4, 2)# Polygon四边形对象 ， 会自动计算四个点 ， 最后四个点顺序为：左上 左下右下 右上 左上quadrilateral_polygon = Polygon(quadrilateral_array).convex_hull?return quadrilateral_array, quadrilateral_polygon?def calculate_iou(actual_quadrilateral, predict_quadrilateral):"""?:param actual_quadrilateral: 预测四边形四个点坐标的一维数组表示 ， [x,y,x,y....]:param predict_quadrilateral: 期望四边形四个点坐标的一维数组表示 ， [x,y,x,y....]:return:"""# 预测四边形二维数组, 预测四边形 Polygon 对象actual_quadrilateral_array, actual_quadrilateral_polygon = to_polygon(actual_quadrilateral)# 期望四边形二维数组, 期望四边形 Polygon 对象predict_quadrilateral_array, predict_quadrilateral_polygon = to_polygon(predict_quadrilateral)?# 合并两个box坐标 ， 变为8*2 便于后面计算并集面积union_poly = np.concatenate((actual_quadrilateral_array, predict_quadrilateral_array))# 两两四边形是否存在交集inter_status = actual_quadrilateral_polygon.intersects(predict_quadrilateral_polygon)# 如果两四边形相交 ， 则进iou计算if inter_status:try:# 交集面积inter_area = actual_quadrilateral_polygon.intersection(predict_quadrilateral_polygon).area# 并集面积 计算方式一#union_area = poly1.area + poly2.area - inter_area# 并集面积 计算方式二union_area = MultiPoint(union_poly).convex_hull.area# 若并集面积等于0,则iou = 0if union_area == 0:iou = 0else:# 第一种计算的是: 交集部分/包含两个四边形最小多边形的面积iou = float(inter_area) / union_area#第二种： 交集 / 并集（常见矩形框IOU计算方式）# iou=float(inter_area) /(poly1.area+poly2.area-inter_area)except shapely.errors.TopologicalError :print('shapely.errors.TopologicalError occured, iou set to 0')iou = 0else:iou = 0?return iou?if __name__ == '__main__':actual_quadrilateral = [908, 215, 934, 312, 752, 355, 728, 252]predict_quadrilateral =[923, 308, 758, 342, 741, 262, 907, 228]iou = calculate_iou(actual_quadrilateral, predict_quadrilateral)print(iou)

避坑指南运行代码抛出 WinError 126 错误