现在 ， 让我们暂时抛开随机性的问题 ， 我们来从编程的角度去考虑它 。 我们可以将随机数发生器（RNG）定义为可以输出一系列数字的东西 。 为了确保它们尽可能的随机 ， 我们还将引入一些新的东西 ， 比如说“状态” 。 当“状态”被传递到这个RNG函数中时 ， 除了输出一个随机数之外 ， 它还将输出一个新的“状态” 。 接下来 ， 我们可以把这个输出的“状态”重新传递给RNG ， 然后继续生成下一个随机数 ， 然后又拿到一个新的“状态” ， 如此反复 ， 最终得到我们想要的随机数字 。
随机数发生器（RNG）是由冯·诺依曼（Von Neumann）在20世纪40年代的某个时候发明的 ， 因此RNG的标准相对来说还是有点古老了 。 其中 ， 需要对N位数进行平方计算 ， 然后计算的结果中取N/2个中间数字作为输出以及下一次迭代的“状态”平方 。 举个简单的例子 ， 我们取n=2 ， 其工作原理如下：我们从43开始 ， 平方得到1849 ， 然后去中间的两个数字得到结果为84 。 此时 ， 数字84就是我们的新“状态” ， 接下来继续取该“状态”的平方 ， 得到7056 ， 取中间值得到05 ， 然后继续输出新的“状态” 。 接下来得到的就是25 ， 这里我们标记为0025 ， 给到我们的新“状态”为2 ， 然后继续计算得到0004 ， 这里就被标记成了0 ， 以此类推…
大家看 ， 这里我们好像进入了一个死循环 。 0的平方当然是0 ， 这就好像不那么随机了 。 事实上 ， 不管你从哪个数字开始 ， 这种行为都是很糟糕的 。 下表列出了所有状态/输出 ， 表明向循环方向退化的趋势是不可避免的：
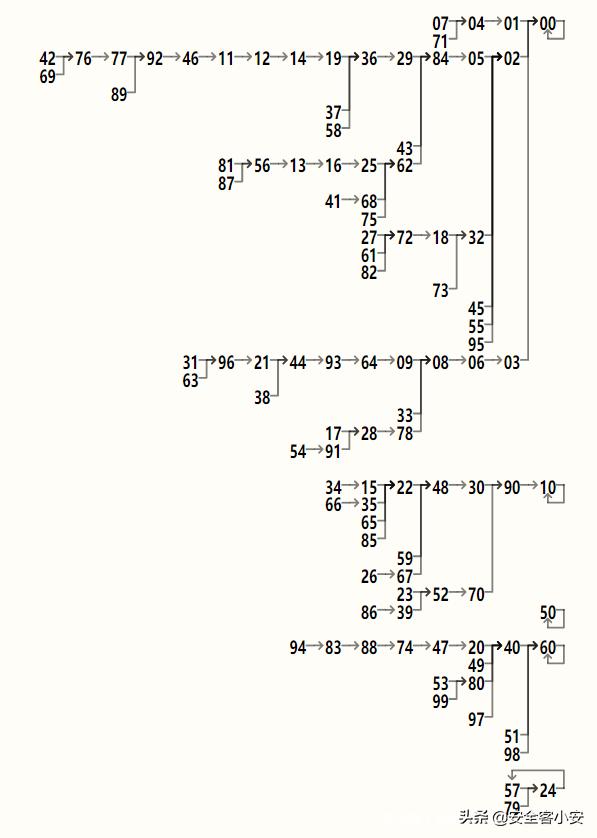文章插图
对于“状态”为4位数的版本 ， 性能更好 ， 相关伪代码如下：
def von_neumann_generator(state): """The version with a 4 digit state/output not to be confused with the one above, that has two.""" #e.g. 1234**2->1522756 square = state**2#1522756 -> 01522756 formattedSquare = "%08d" % square #01522756 -> 5227 next_state = output = int(formattedSquare[2:6]) return (next_state,output)state = 1234for i in range(20): state,output = von_neumann_generator(state) print(output)在上面的例子中 ， 您可以看到状态和输出是相同的 ， 但是没有特别的原因必须这样做 。 例如 ， 我们可以将状态设置为内部四个数字 ， 输出为外部四个数字：
def much_better_von_neumann_generator(state): square = state**2 # e.g. 1234**2->1522756 formattedSquare = "%08d"%square output = int(formattedSquare[0:2]+formattedSquare[6:]) next_state = int(formattedSquare[2:6]) return (next_state,output)state = 1234for i in range(40): state,output = much_better_von_neumann_generator(state) print(output)虽然这个RNG还不是最安全的状态 ， 但随机数的输出和“状态”之间的关系已经很难去预测了 。 然而 ， 它们在某种因果意义上显然是相互关联的 。 现在 ， 我们已经逐渐开始看到RNG设计中的一些关键矛盾点了：
不可预测性–增加输出/状态中的位数会增加输出的不可预测性 。 有时设计不太成熟的算法（如上面的算法）最终会退化为某种不安全的低随机性状态 ， 但在计算机中使用的大多数算法在返回到原始状态之前 ， 会以某种顺序简单地迭代整个状态 。 比如说 ， 我们可以通过计算位数来验证生成的随机数是均匀分布的 ， 这里就不得不提到加密安全的伪随机数发生器（CSPRNGS） 。
性能–不幸的是 ， CSPRNGs非常慢 。 而高性能RNG相比来说则更为常见 ， 几乎每个网站都在不断地向访问或登录的用户发送一系列随机数字 ， 而在网络游戏中 ， 它们更是无处不在 。 因此 ， 仅仅使用CSPRNG并不一定是正确的 。 也就是说 ， 现在使用的高性能算法比我上面演示的算法要好得多 。
政治方面-这就不适合在这里详细讨论了 ， 有些地方的当局会要求开发人员使用他们所定义的所谓的“超级安全”的RNG标准 ， 但实际上这些标准都是存在后门的 。 这一点大家心里清楚就好了 ， 毕竟之前也被曝光过 。
后话在《神经网络与随机数的安全性分析（上）》中 ， 我们对随机数发生器（RNG）的安全方面进行了讨论 ， 后续内容我们将在《神经网络与随机数的安全性分析（下）》中与大家继续讨论 ， 请大家及时关注安全客的最新发布 。
欢迎登录安全客 -有思想的安全新媒体www.anquanke.com/加入交流群1015601496 获取更多最新资讯
原文链接：

稿源：(未知)

【傻大方】网址：http://www.shadafang.com/c/111J2R642020.html

标题：神经网络与随机数的安全性分析（上）( 二 )