这是我打印的输出（出于本教程的目的 ， 我摆脱了That和n_eff）：
Inference for Stan model: anon_model_3112a6cce1c41eead6e39aa4b53ccc8b.8 chains, each with iter=6000; warmup=3000; thin=1; post-warmup draws per chain=3000, total post-warmup draws=24000.mean se_meansd2.5%25%50%75%97.5%alpha-8.350.023.81 -15.79 -10.93-8.37-5.74-0.97beta[1]-0.481.9e-30.33-1.12-0.7-0.48-0.260.17beta[2]0.024.6e-5 7.9e-3 6.1e-30.020.020.030.04beta[3]-0.028.7e-50.01-0.04-0.03-0.02-6.9e-30.01beta[4]-7.0e-34.0e-6 7.0e-4-8.3e-3-7.4e-3-7.0e-3-6.5e-3-5.6e-3beta[5]0.15.9e-40.1-0.10.030.10.170.3beta[6]0.692.7e-40.050.60.650.690.720.78beta[7]-1.752.9e-30.51-2.73-2.09-1.75-1.41-0.73beta[8]0.362.7e-30.51-0.640.020.360.711.38sigma3.337.6e-40.133.093.243.323.413.59y_new[1]26.130.023.3719.5923.8526.1128.3932.75y_new[2]25.380.023.3618.8323.1225.3727.6531.95......theta[1]24.752.7e-30.4723.8324.4424.7525.0725.68theta[2]19.592.6e-30.4318.7619.319.5919.8820.43 ......fit.stansummary（）是一个像表一样排列的字符串 ， 它为我提供了拟合期间估计的每个参数的后验均值 ， 标准差和几个百分点 。虽然alpha对应于截距 ， 但我们有8个beta回归变量 ， 复杂度或观察误差sigma ， 训练集theta的拟合值以及测试集y_new的预测值 。
诊断在幕后运行MCMC ， 至关重要的是我们要以图表的形式检查基本诊断 。对于这些情节 ， 我依靠出色的arviz库进行贝叶斯可视化（与PyMC3和pystan同样有效） 。
· 链混合-轨迹图 。这些系列图应显示在实线中"合理大小"的间隔内振荡的"厚发"链 ， 以指示良好的混合 。"稀疏的"链意味着MCMC无法有效地进行探索 ， 并且可能陷入某些异常情况 。
ax = az.plot_trace(fit, var_names=["alpha","beta","sigma"])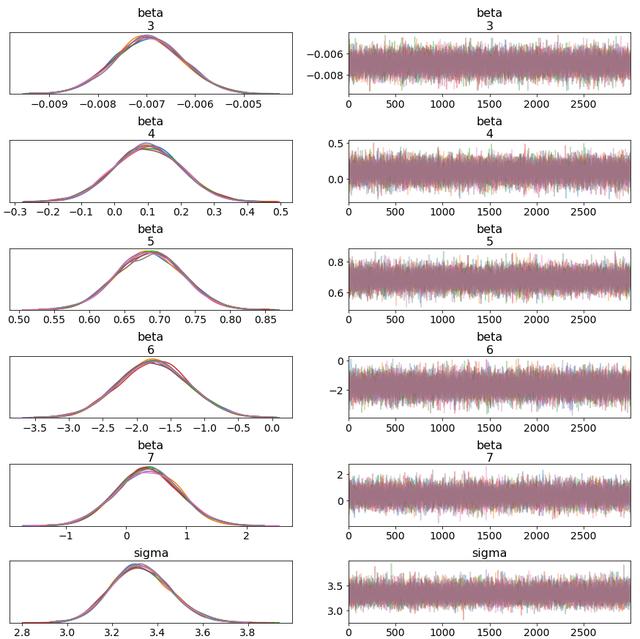文章插图
Thick-haired chains ! I omitted alpha and beta[1:2] due to image size.
· 我们参数的后可信区间-森林图 。这些应该作为我们模型参数（和超参数！）的比例和位置的直观指南 。例如 ， σ（此处为PC框架[4]下的复杂度参数）不应低于0 ， 而如果?个预测变量的可信区间不包含0 ， 或者如果0 ， 则我们可以了解"统计意义" 几乎不在里面
axes = az.plot_forest(post_data,kind="forestplot",var_names= ["beta","sigma"],combined=True,ridgeplot_overlap=1.5,colors="blue",figsize=(9, 4),)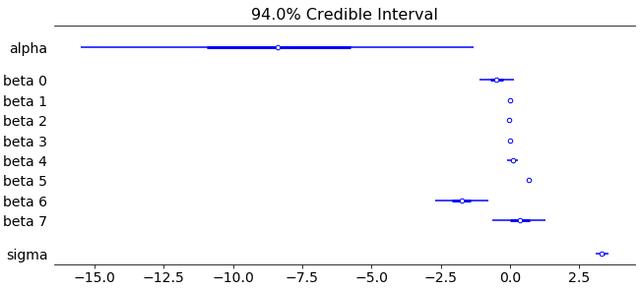文章插图
Looks good. alpha here can be seen as "collector" representing our reference category (I used reference encoding). We can certainly normalize our variables for friendlier scaling — I encourage you to play with this.
预测贝叶斯推断具有预测能力 ， 我们可以通过从预测后验分布中采样来产生它们：
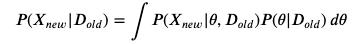文章插图
这些（以及整个贝叶斯框架）的优点在于 ， 我们可以使用（预测的）可信区间来了解估计的方差/波动性 。毕竟 ， 如果预测模型的预测"足够接近"目标50的1倍 ， 那么预测模型有什么用？
让我们看看我们的预测值如何与测试集中的观察值进行比较：
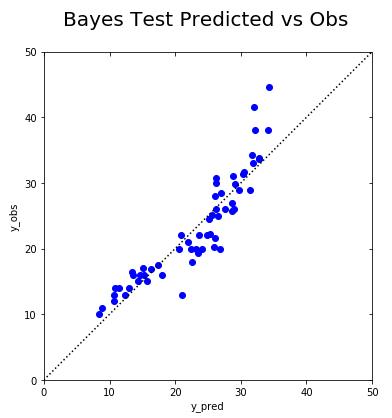文章插图
The straight dotted line indicates perfect prediction. We're not too far from it.
然后 ， 我们可以对这些预测进行ML标准度量（MSE） ， 以根据保留的测试集中的实际值评估其质量 。
当我们更改一些模型输入时 ， 我们还可以可视化我们的预测值（以及它们相应的95％可信度区间）：
az.style.use("arviz-darkgrid")sns.relplot(x="weight", y="mpg")data=http://kandian.youth.cn/index/pd.DataFrame({'weight':X_test['weight'],'mpg':y_test}))az.plot_hpd(X_test['weight'], la['y_new'], color="k", plot_kwargs={"ls": "--"})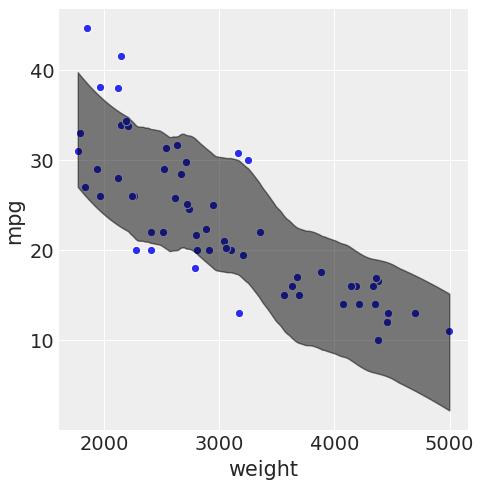文章插图
sns.relplot(x="acceleration", y="mpg",data=http://kandian.youth.cn/index/pd.DataFrame({'acceleration':X_test['acceleration'],'mpg':y_test}))az.plot_hpd(X_test['acceleration'], la['y_new'], color="k", plot_kwargs={"ls": "--"})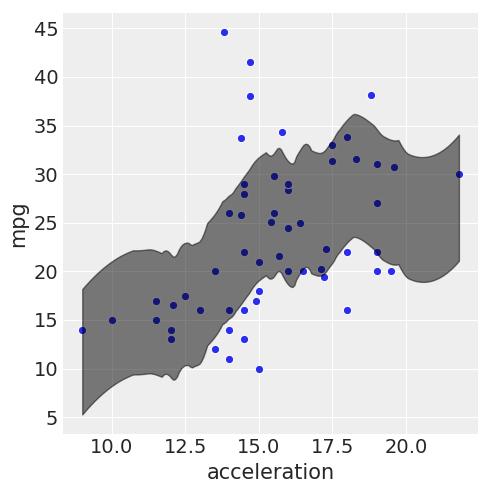文章插图
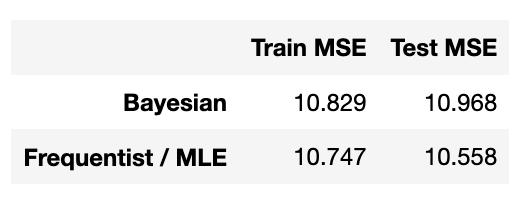
在下面 ， 我使用统计模型将贝叶斯模型的性能与普通最大似然线性回归模型的性能进行比较：
文章插图
They perform painfully close (for this particular seed).
最佳实践：为了更好地了解模型性能 ， 您应该通过对K≥30的火车测试拆分运行实现 ， 在测试MSE上引导95％置信区间（CLT） 。

稿源：(未知)

【傻大方】网址：http://www.shadafang.com/c/111J2V402020.html

标题：一文看懂如何使用（Py）Stan进行贝叶斯推理( 三 )