文章插图
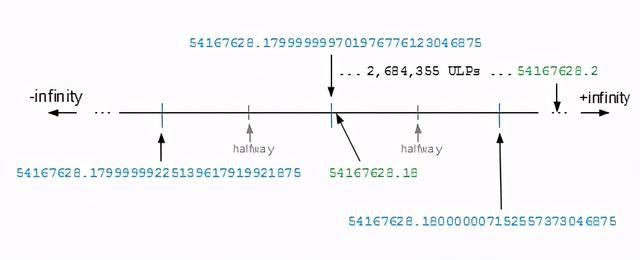
示例：最短的十进制字符串为10位
示例4：仅需要15位数字浮点数9161196241250.05078125可以四舍五入到15位（9161196241250.05） ， 并且仍然是双向的 。 当然 ， 它也将四舍五入为17位数字（9161196241250.0508）和16位数字（9161196241250.051） ， 这已在图中显示 。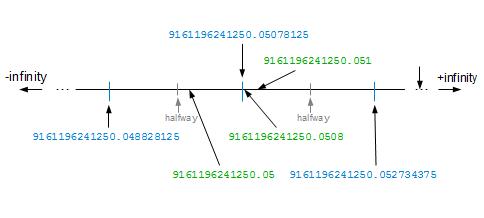
文章插图
示例：最短的十进制字符串为15位
在此示例中 ， 四舍五入为17位数字表示一个17位数字的字符串 ， 四舍五入为16位数字表示为16位数字的字符串 ， 而四舍五入为15位数字则为15位数字的字符串 。 这与示例3不同 ， 示例3中无论将其舍入为17、16、15、14、13、12、11或10位 ， 都将54167628.17999999970970776776123046875舍入到10位字符串54167628.18 。
接下来来解释下为什么？
四舍五入的最短十进制字符串可能不是最近的可以使用最多17个有效十进制数字来标识任何双精度浮点数 。 这意味着 ， 如果将浮点数转换为十进制字符串 ， 将其（最接近）四舍五入为17位数字 ， 然后再将其转换回浮点数 ， 则将恢复原始浮点数 。 换句话说 ， 转换是往返可逆的 。
有时（很多）少于17位数字将用于往返；通常希望找到最短的此类字符串 。 一些编程语言生成最短的十进制字符串 ， 但许多不生成 。 确认语言是什么规则的方法是 ， 将浮点数四舍五入为递增长度的十进制字符串 ， 然后每次检查字符串往返是否可逆 。 对于双精度 ， 你需要四舍五入到15位数字 ， 然后如果需要则四舍五入到16位数字 ， 如果需要 ， 最后四舍五入到17位数字 。
问题根源：2的幂让我们在2 -44上尝试蛮力算法 ， 该算法的十六进制浮点常量为0x1p-44 ， 而全精度十进制值为5.684341886080801486968994140625e-14 。 四舍五入为15位数字 ， 它是5.6843418860808e-14 ， 但这不是往返可逆的：它转换为0x1.ffffffffffffep-45 。 四舍五入为16位数字 ， 它是5.684341886080801e-14 ， 但这也不是往返的：它转换为0x1.fffffffffffffp-45 。 因此 ， 必须使用17位标示数字5.6843418860808015e-14 。
可是等等！有往返的16位数字 ， 我们错过了：5.684341886080802e-14 。 为什么没有更接近的16位数字 ， 却要往返呢？
问题的根源在于二进制浮点数之间的间隙大小以两个边界的幂变化 。 大于2的幂的间隙大小是小于2的幂的间隙大小的两倍 。 这种不对称是必要的条件 ， 但它本身并不会导致问题 。 以及两个因子的幂附近的十进制数字之间的差距的大小 。 对于双精度 ， 有问题的十进制间隙大小仅出现在16位数字上 。
即使对于16位数字 ， 并不是所有的2的幂都表现出异常 。 二进制和十进制数字必须以某种方式对齐 。 对于初学者 ， 最接近的16位十进制数字必须低于2的幂 ， 而下一个更高的16位十进制数字必须高于2的幂 。 此外 ， 最接近的16位十进制数必须比下一个较低的53位二进制数大一半（不能为中位数 ， 因为舍入至最接近偶数会将其映射为2的幂） ， 而下一个较高的16位十进制数不能超过下一个较高的53位二进制数的一半 。 由于中途距离在2的幂的任一侧都不相同 ， 因此 ， 越远的十进制数将映射到2的幂 ， 但越小的十进制数则不会 。
下图按比例绘制 ， 描述了示例的情况：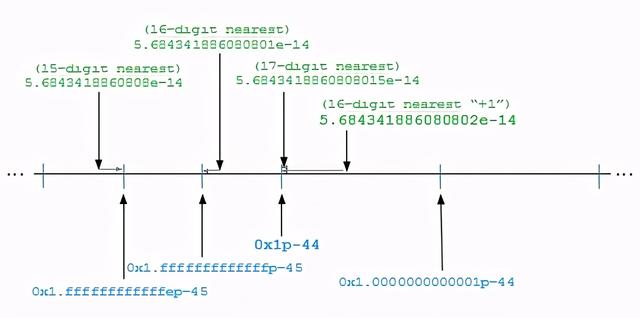
文章插图
示例：最短的十进制字符串不是最近的
该图显示了从2 -45指数到2 -44指数范围的53位二进制浮点数 。 这在16位数浮点十进制数的10 -14范围内发生 。 二进制间隙变化的从大小2 （-45 + 1-53） = 2 -97 ≈ 6.3×10 -30?2 （-44 + 1-53） = 2 -96 ≈ 1.3×10 -29 。 在该范围内的小数位间隔保持恒定为10 （-14 + 1-16） = 10 -29 。 问题就在这里 。 十进制间隙大小介于两个二进制间隙大小之间 。
当出现十进制间隙大小时有问题的十进制间隙大小仅适用于16位十进制数字 。 这是因为对于15位以下的十进制数字 ， 十进制间隙大小大于最大的双精度二进制间隙大小 ， 对于17位以上的十进制数字 ， 十进制间隙大小小于最小的双精度大小 。 二进制间隙大小 。 后两个事实分别是往返十进制到浮点到十进制以及浮点到十进制到浮点转换的结果 。
发生的所有两种力量我编写了一个C程序来测试正常双精度范围内2的所有1046次幂：2 -1022到2 1023 。 对于54 ， 最接近的16位数字不能往返 ， 但是下一位数可以：
2 976 ， 2 966 ， 2 956 ， 2 896 ， 2 890 ， 2 863 ， 2 803 ， 2 740 ， 2 710 ， 2 594 ， 2 574 ， 2 554 ， 2 544 ， 2 534 ， 2 481 ， 2 405 ， 2 398 ， 2 378 ， 2 345 ， 2 305 ， 2 275 ， 2 182 ， 2 172 ， 2 149 ， 2 132 ， 2 122 ， 289 ， 2 -24 ， 2 -44 ， 2 -77 ， 2 -97 ， 2 -140 ， 2 -296 ， 2 -366 ， 2 -383 ， 2 -489 ， 2 -496 ， 2 -499 ， 2 -509 ，2 -549 ， 2 -569 ， 2 -645 ， 2 -652 ， 2 -662 ， 2 -695 ， 2 -705 ， 2 -778 ， 2 -788 ， 2 -791 ， 2 -808 ， 2 -921 ， 2 - 957 ， 2-1007 ， 2 -1017

• 逛逛|淘宝内容化再升级：“买家秀”变身“逛逛”试图冲破算法局限
• 算法|【远见】个人信息保护法将出台 揭开数据算法的神秘“面纱”
• 创园|中国V谷的云存储之道，马栏山文创园将视频处理效率提升6倍
• Store|苹果聘请知名风投家Josh Elman改进App Store
• 出行|嘀嗒出行“出租车·新出行”提升运营效率降低空驶率增加司机收入
• 能力|美国研发快速法评估神经网络的不确定性 改进自动驾驶车决策能力
• 复习|期末整理复习笔记？MHMO魅蒙iPad专用笔助提高效率
• 算法|为什么长视频没有强算法推荐的产品
• 三星|曝三星 Galaxy Z Fold3 定价与 Fold2 相同但将新增大量改进
• 数据结构与算法系列 - 深度优先和广度优先