算法|推荐算法改版前的AB测试( 二 ) 假设|推荐|测试|改版

假设我们认为，如果新的推荐算法，比原推荐算法，显著高于5%以上，则可将新推荐算法发布至生产环境。
此时我们可以得到假设：
原假设H0：π2-π1≤5%
备择假设H1：π2-π1＞5%
2）确定显著性水平α
本次实验中，α 值设定 0.05（5%），这是假设检验中最常用的小概率标准值；表示原假设为真时，拒绝原假设的概率。
3）确定临界值
临界值是显著性水平对应的标准正态分布的分位数，显著性水平0.05的情况下，单侧检验对应的标准正态分布的分位数是1.645，双侧检验的标准正态分布的分位数为1.96。
4）收集实验数据，得出结论
【 算法|推荐算法改版前的AB测试】由样本值求得检验统计量的优化指标的数值。若观察值在拒绝域内，则拒绝原假设H0，否则接受原假设H1。
四、开始测试并分析数据定义新推荐算法的准确率为π1，新推荐算法的准确率为π2。
Ho：π1-π2≤5%
H1：π1-π2＞5%
实验目标人群：从进入商城，且使用了“为你推荐”功能的用户流量（UV）中，随机抽取5%，作为实验目标人群；其中的50%为实验组，50%为对照组。
实验时间：1周
假设检验方式：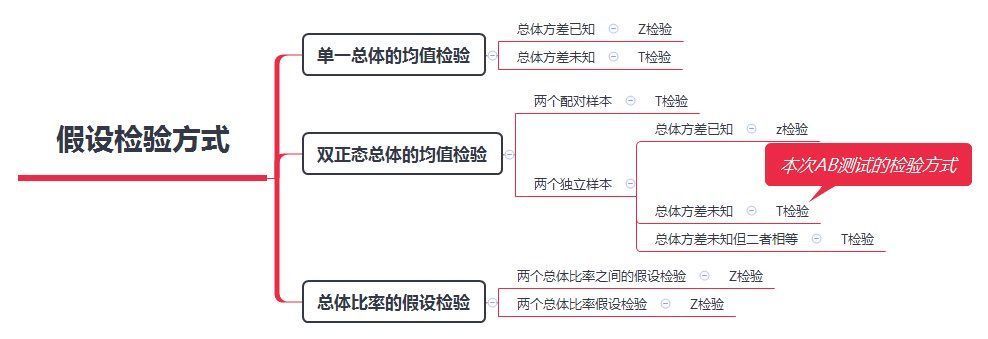

文章插图
不同的AB测试场景，适用于不同的检验方式，如上图所示。
本次AB测试，由于两个推荐系统版本是独立的，且样本数足够大，认为满足正态分布。
根据HO、H1的假设，可判断本次检验为两个独立样本的总体均值的单侧检验，且总体方差未知，需要用样本方差代替总体方差。
此时计算统计量公式为：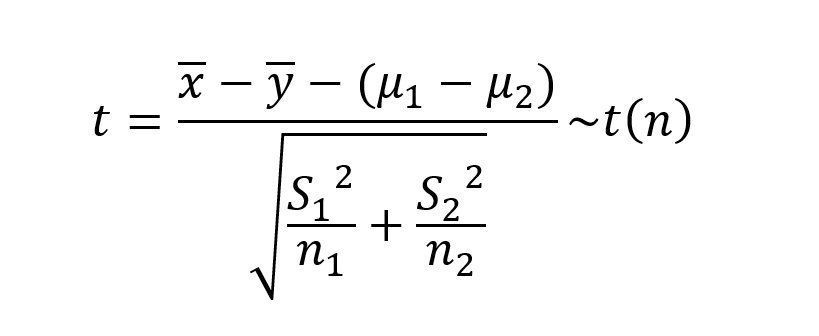

文章插图
显著性水平：0.05。
临界值：在显著性水平为0.05时，单侧检验的临界值Zα为1.645。
实验数据(为方便计算）：实验一周后，有10000用户，使用新推荐算法，准确率的平均值为41%，标准差为20%；有10000用户，使用原推荐算法，准确率的平均值为35%，标准差为10%。此时新算法的准确率定义为x，则x的平均值=41%，原算法的推荐率定义为y，则y的平均值=35%。
计算检验统计量：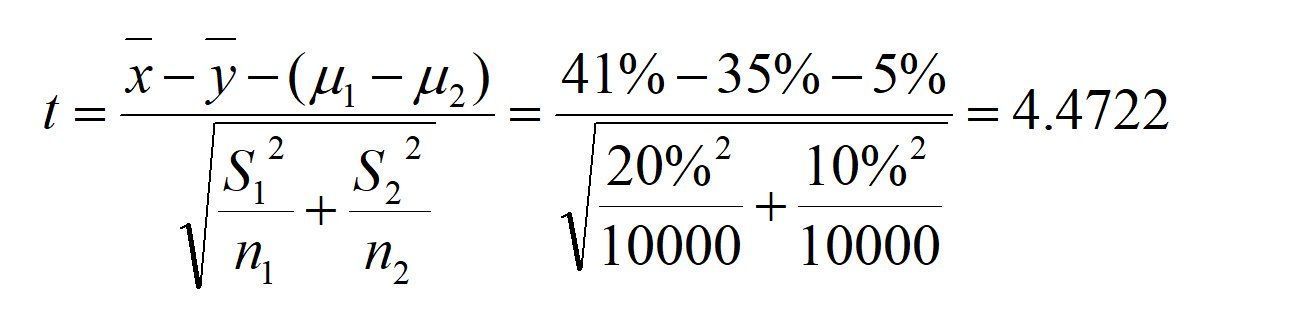

文章插图
检验结果：统计量Z=4.4722，临界值Zα=1.645.由于统计量的值大于临界值而落入拒绝域内，所以拒绝原假设H0，认为新推荐算法的准确率，比原推荐算法显著高出5%，新版本算法可发布至生产环境。
本文由 @16哥原创发布于人人都是产品经理，未经许可，禁止转载。
题图来自 unsplash，基于 CC0 协议