无惧分辨率变化，求解PDE家族：加州理工提傅里叶神经算子方法( 二 ) 机器之心报道编辑：魔王、小

神经算子
神经算子是一个迭代结构 v_0 |→ v_1 |→ . . . |→ v_T ，其中， v_j (j = 0, 1, . . . , T ? 1) 是一系列函数，每一个函数取值于 R^dv 。首先通过局部（逐点）变换 P 将输入 a ∈ A 转换为更高维度的表示 v_0 = P(a) 。这一局部变换 P 一般通过浅层全连接网络进行参数化， P : R^da → R^dv 单独对每个空间组件 a(x) ∈ R^da 执行。类似地，输出 u = Q(v_T ) 是 v_T 通过局部变换 Q : R^dv → R^du 后的投影。
在每次迭代中，更新 v_t |→ v_t+1 被定义为非局部积分算子 K 和局部非线性激活函数 σ 的组合。
文章插图
κ_φ 是从数据中学得的核函数。定义 1 和定义 2 构成了神经网络向无限维空间的泛化 [Li et al., 2020b] 。如果我们移除对函数 a 的依赖，并使 κ_φ(x, y) = κ_φ(x?y) ，则得到 (4) 是卷积算子。
研究者在傅里叶空间中直接参数化 κ_φ ，并使用快速傅里叶变换（FFT）对 (4) 进行高效计算，从而得到在 PDE 问题上获得 SOTA 结果的新型快速架构。
傅里叶神经算子
研究人员提出用傅里叶空间中定义的卷积算子替换掉 (4) 中的核积分算子。令 F 表示对函数的傅里叶变换 f : D → R^dv ， F^?1 表示逆变换，则得到：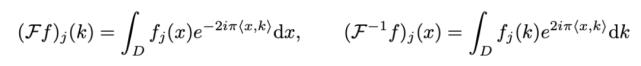
文章插图
j = 1, . . . , d_v ， i = √?1 表示虚数单位。令公式 (4) 中的 κ_φ(x, y, a(x), a(y)) = κ_φ(x ? y) ，并应用卷积定理，得到：
从而在傅里叶空间中直接参数化 κ_φ：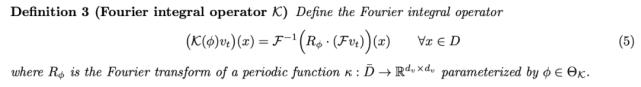
文章插图
实验
研究者在一维伯格斯方程、二维达西流动问题和二维纳维 - 斯托克斯方程上对比了 FNO 和多个有限维架构和基于算子的逼近方法。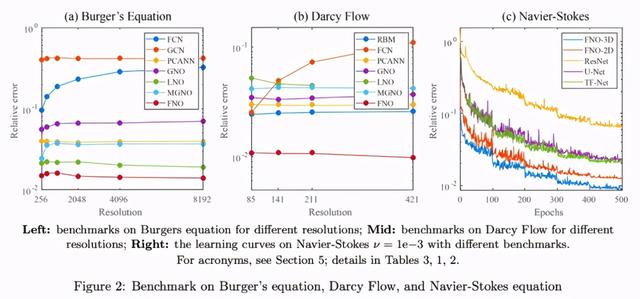
文章插图
伯格斯方程
该实验的结果参见图 2a 和表 1 。
该研究提出的 FNO 方法取得了最低的相对误差，并且该误差值不随分辨率的变化而变化，而基于卷积神经网络的方法（FCN）的误差随着分辨率的增长而增大。与其他神经算子方法（如在物理空间中使用 Nystr?m 采样的 GNO 和 MGNO）相比，傅里叶神经算子方法在准确率和计算效率方面均更胜一筹。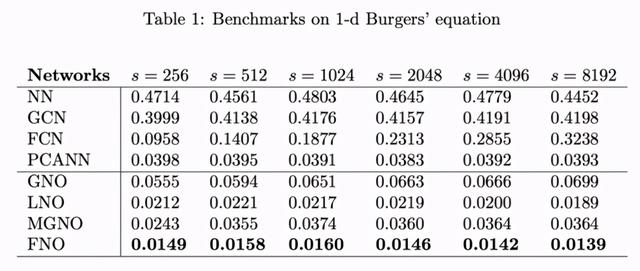
文章插图
达西流动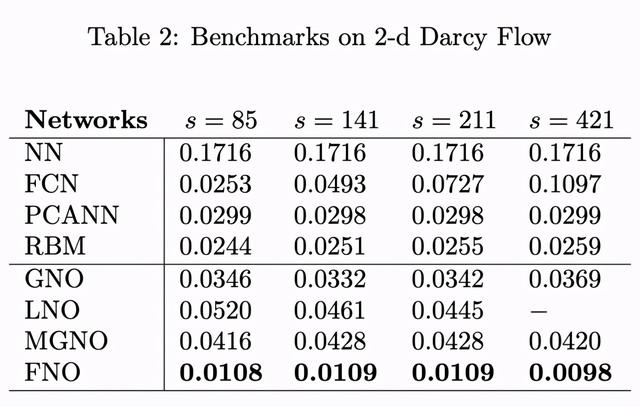
文章插图
该实验结果参见图 2b 和表 2 。 FNO 方法的相对误差比其他方法几乎低了一个数量级，而且该误差值并不会随着分辨率的变化而变化。
纳维 - 斯托克斯方程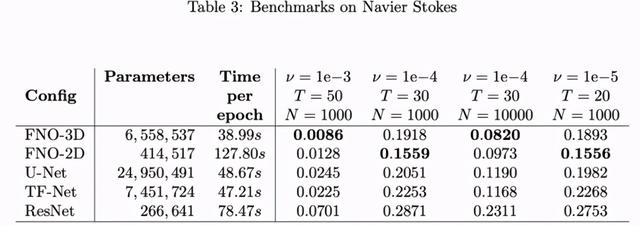
文章插图
如表 3 所示，在具备足够数据时（ν = 1e?3, N = 1000 和 ν = 1e?4, N = 10000）， FNO-3D 展现出了最优性能。对于数据不足的情况（ν = 1e?4, N = 1000 和 ν = 1e?5, N = 1000），其他方法误差均大于 15% ，而 FNO-2D 的误差值最低。
此外，该研究在 64 × 64 × 20 数据上训练 FNO-3D ，在 256 × 256 × 80 上进行评估，取得了不错的泛化效果。这表明该方法不仅可泛化至不同的空间分辨率，对时间分辨率也具备泛化性。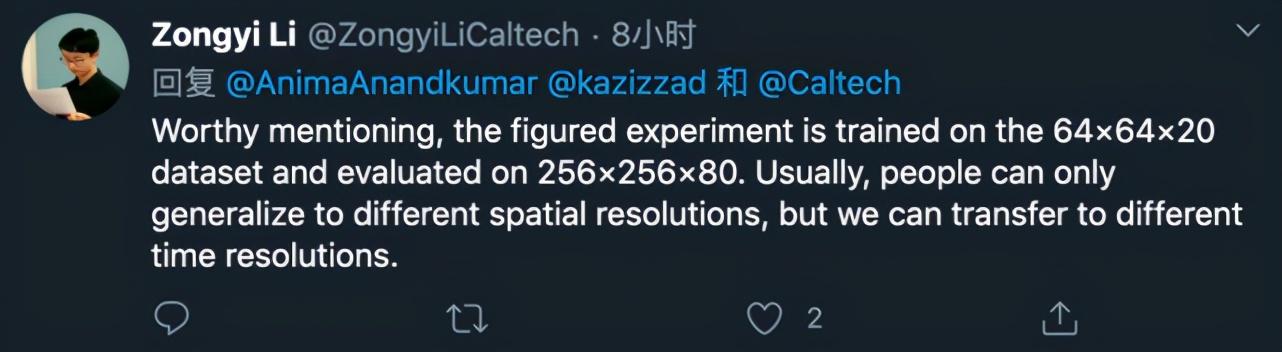
文章插图
贝叶斯逆问题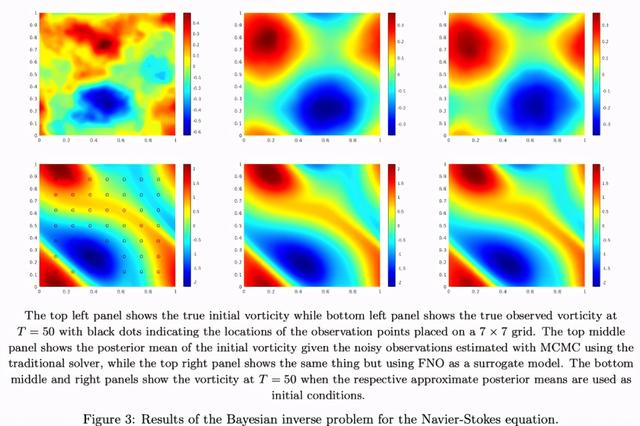
文章插图
如上图 3 所示， FNO 和传统的 PDE 求解器可以恢复几乎相同的后验均值。但是， FNO 只需 0.005s 即可评估一个实例，而经过优化的传统求解器仍需要 2.2s 。使用 FNO 的 MCMC 一共用时两分半，而使用传统求解器的 MCMC 则用时超过 18 个小时。
第一作者简介
【无惧分辨率变化，求解PDE家族：加州理工提傅里叶神经算子方法】该研究的第一作者 Zongyi Li ，目前是加州理工学院计算机和数学系的在读博士生。他的研究方向为机器学习、理论计算科学和应用数学。最近，他一直致力于为偏微分方程研究图神经网络。
文章插图
在来到加州理工之前， Zongyi Li 毕业于圣路易斯华盛顿大学（Washington University in St. Louis），主修计算机科学和数学，导师为 Brendan Juba 和 Xiang Tang 。