介绍神经网络背后的数学( 二 )

令y = [y ， y 2 ， …y?]和?= [ ， ?2 ， …??]是实际值和预测值的行向量。因此，上述方程简化为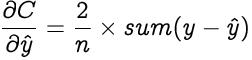
文章插图
现在，让我们找到预测值相对于z的梯度。这会有点冗长。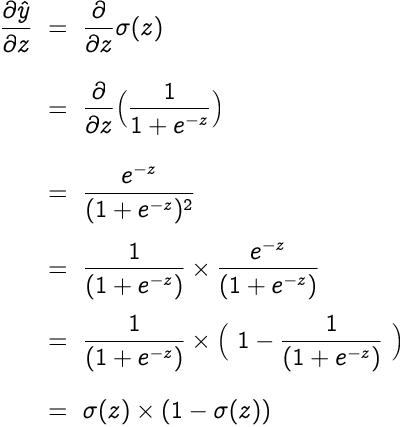
文章插图
z相对于权重w?的梯度为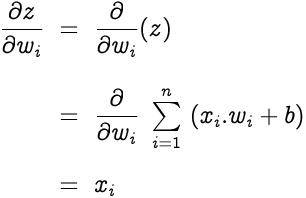
文章插图
因此我们得到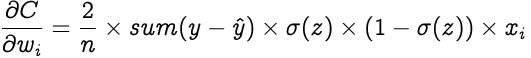
文章插图
偏见呢？ —理论上，偏置被认为具有恒定值1的输入。因此，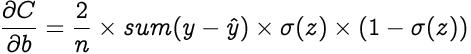
文章插图
优化：优化是从某些可用替代方案中选择最佳元素，在我们的案例中，优化是选择感知器的最佳权重和偏差。让我们选择梯度下降作为我们的优化算法，该算法会更改权重和偏差，与权重函数相对于相应权重或偏差的梯度负值成比例。学习率（α）是一个超参数，用于控制权重和偏差的变化量。
权重和偏差更新如下，重复进行反向传播和梯度下降直到收敛。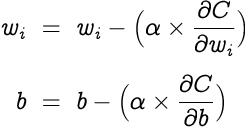
文章插图
最后的想法希望您对本文有所了解，并理解神经网络和深度学习背后的数学原理。我已经在本文中解释了单个神经元的工作。但是，这些基本概念经过一些修改后适用于所有类型的神经网络。
(本文翻译自Martin Heinz的文章《An Introduction To Mathematics Behind Neural Networks》，参考：)