没有完整图时，如何使用图深度学习？需要了解流形学习2.0版本( 二 ) 机器之心编译编辑：陈萍流形

流形学习
DGCNN 和 DGM 在概念上与流形学习或非线性降维算法相似，流形学习很早就已出现并流行，且目前仍用于数据可视化。流形学习方法的基本假设是数据具有内在的低维结构。虽然数据可以在数百甚至数千维的空间中表示，但它却只有几个自由度，示例如下：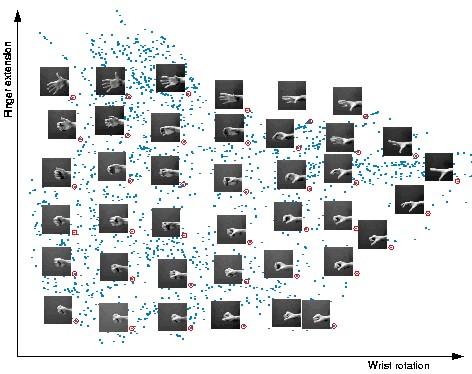
文章插图
虽然这个数据集中的手部图像是高维的（64x64 像素构成 4096 个维度），但它们本质上是低维的，可以用两个自由度来解释：手腕旋转和手指伸展。流形学习算法能够捕捉数据集的这种内在低维结构，并将其在欧几里德空间中进行表示。（图源 [9]）
再比如球面上的一点（即三维欧式空间上的点），可以用三元组来表示其坐标：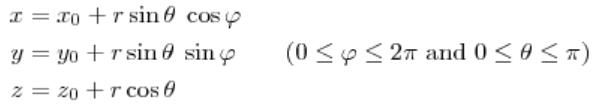
文章插图
但事实上这个三维坐标只有两个变量 θ 和 φ ，也可以说它的自由度为 2 ，正好对应了它是一个二维的流形。
流形学习的目的是捕捉这些自由度，并将数据的维数降至其固有维数。流形学习与 PCA 等线性降维方法的重要区别在于，由于数据的非欧几里德结构，我们可能无法通过线性投影恢复流形。如下图所示，线性降维（左）为线性降维，流形学习（右）为非线性降维。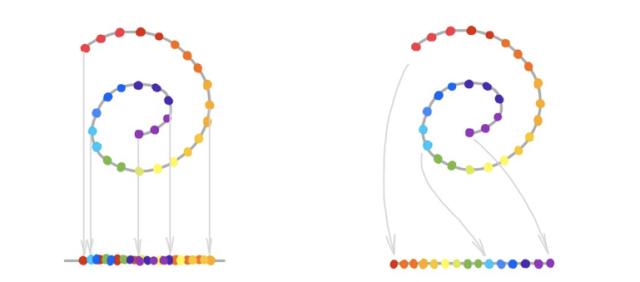
文章插图
流形学习算法在恢复「流形」方法上各不相同，但它们有一个共同的蓝图。
首先，创建一个数据表示，通过构造一个 k 近邻图来获取其局部结构。其次，计算数据的低维表示（嵌入），并试图保留原始数据的结构。这是大多数流形学习方法的区别所在。这种新的表示将原来的非欧几里德结构「展平」成一个更容易处理的欧几里德空间。第三，一旦计算出表示，就会对其应用机器学习算法（通常是聚类）。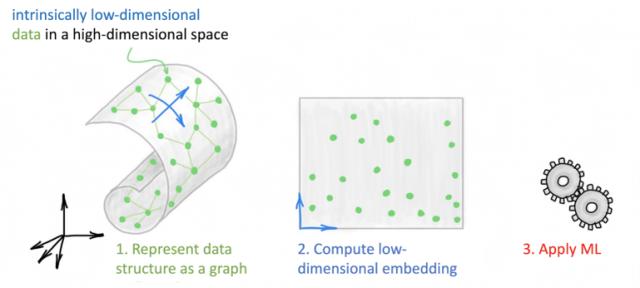
文章插图
多种流形学习方法的蓝图：首先，将数据表示为图；其次，计算该图的低维嵌入；第三，将 ML 算法应用于这种低维表示。
这其中面临的一项挑战是图构建与 ML 算法的分离，有时需要精确的参数调整（例如邻域数或邻域半径），以确定如何构建图才能使下游任务正常运行。流形学习算法更严重的缺点或许是：数据很少表示为低维的原始形式。例如，在处理图像时，必须使用各种人工制定的特征提取技术作为预处理步骤。
图深度学习提供了一种现代方法，即用单个图神经网络代替上文提到的三个阶段。例如，在 DGCNN 或 DGM 中，图的构造和学习是同一架构的一部分：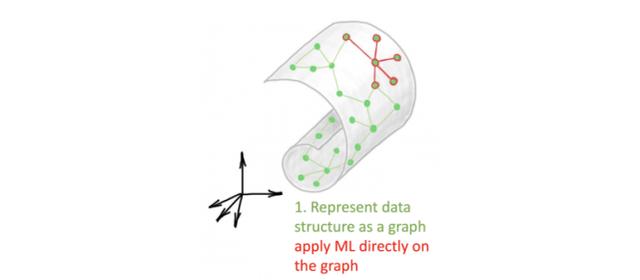
文章插图
潜图学习可以看作是流形学习问题的一种现代设置，在这里，图被学习并用作某些下游任务优化的端到端 GNN pipeline 的一部分。
这种方法的吸引力在于：将单个数据点和它们所在的空间结合在相同的 pipeline 中。在图像的例子中，我们可以使用传统的 CNN 从每个图像中提取视觉特征，并使用 GNN 来建模它们之间的关系。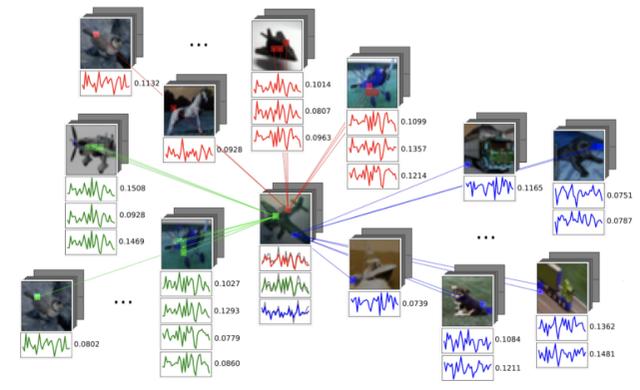
文章插图
PeerNet 是标准 CNN 中基于图的正则化层，可聚合来自多个图像的相似像素，从而降低对对抗性扰动的敏感性。（图源 [12]）
潜图学习的其它应用
潜图学习还有许多其他有趣的应用。
第一是少样本学习：利用基于图的方法从少量样本中进行归纳（重点：只需要少量带有标注的样本）。在计算机视觉中，数据标注量从几千到上万不等，成本很高，因此少样本学习变得越来越重要。
第二是生物学领域：人们经常通过实验观察生物分子如蛋白质的表达水平，并试图重建它们的相互作用和信号网络。
第三是对物理系统的分析：其中图可以描述多个对象之间的交互作用。尤其是处理复杂粒子相互作用的物理学家，最近对基于图的方法表现出了浓厚的兴趣。
第四是 NLP 问题：在 NLP 领域中，图神经网络可以看作是 transformer 架构的泛化。所提到的许多问题也提出了在图结构中加入先验知识，这一结构在很大程度上仍然是开放的：例如，人们可能希望强迫图遵守某些构造规则或与某些统计模型兼容。
潜图学习，虽然不是全新的领域，但它为旧问题提供了新的视角。对于图机器学习问题而言，这无疑是一个有趣的设置，为 GNN 研究人员提供了新的方向。