程序员必备的基本算法：递归详解( 二 ) 前言递归是一种非常重要的算法思想

//n的阶乘（n为大于0的自然数）int factorial (int n){}2.寻找递归终止条件递归的一个典型特征就是必须有一个终止的条件，即不能无限循环地调用本身。所以，用递归思路去解决问题的时候，就需要寻找递归终止条件是什么。比如阶乘问题，当n=1的时候，不用再往下递归了，可以跳出循环啦， n=1就可以作为递归的终止条件，如下：
//n的阶乘（n为大于0的自然数）int factorial (int n){if(n==1){return 1;}}3.递推函数的等价关系式递归的「本义」，就是原问题可以拆为同类且更容易解决的子问题，即「原问题和子问题都可以用同一个函数关系表示。递推函数的等价关系式，这个步骤就等价于寻找原问题与子问题的关系，如何用一个公式把这个函数表达清楚」。阶乘的公式就可以表示为 f(n) = n * f(n-1), 因此，阶乘的递归程序代码就可以写成这样，如下：
int factorial (int n){if(n==1){return 1;}return n * factorial(n-1);}「注意啦」，不是所有递推函数的等价关系都像阶乘这么简单，一下子就能推导出来。需要我们多接触，多积累，多思考，多练习递归题目滴~
leetcode案例分析来分析一道leetcode递归的经典题目吧~
?
原题链接在这里哈：
?
「题目：」翻转一棵二叉树。
输入：
4/\27 / \/ \13 69输出：
4/\72 / \/ \96 31我们按照以上递归解题的三板斧来：
「1. 定义函数功能」
函数功能（即这个递归原问题是），给出一颗树，然后翻转它，所以，函数可以定义为：
//翻转一颗二叉树public TreeNode invertTree(TreeNode root) {}/** * Definition for a binary tree node. * public class TreeNode { *int val; *TreeNode left; *TreeNode right; *TreeNode(int x) { val = x; } * } */「2.寻找递归终止条件」
这棵树什么时候不用翻转呢？当然是当前节点为null或者当前节点为叶子节点的时候啦。因此，加上终止条件就是：
//翻转一颗二叉树public TreeNode invertTree(TreeNode root) {if(root==null || (root.left ==null}}「3. 递推函数的等价关系式」
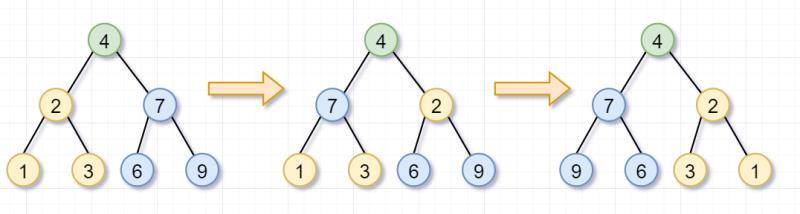
原问题之你要翻转一颗树，是不是可以拆分为子问题，分别翻转它的左子树和右子树？子问题之翻转它的左子树，是不是又可以拆分为，翻转它左子树的左子树以及它左子树的右子树？然后一直翻转到叶子节点为止。嗯，看图理解一下咯~
文章插图
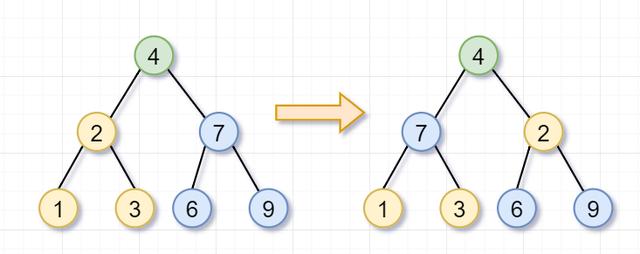
首先，你要翻转根节点为4的树，就需要「翻转它的左子树（根节点为2）和右子树(根节点为7）」。这就是递归的「递」的过程啦
文章插图
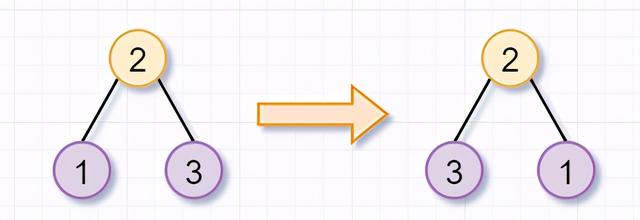
然后呢，根节点为2的树，不是叶子节点，你需要继续「翻转它的左子树（根节点为1）和右子树（根节点为3）」。因为节点1和3都是「叶子节点」了，所以就返回啦。这也是递归的「递」的过程~
文章插图
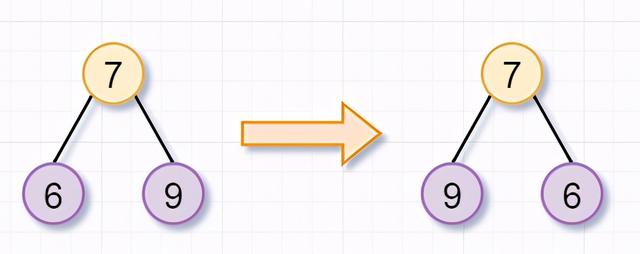
同理，根节点为7的树，也不是叶子节点，你需要翻转「它的左子树（根节点为6）和右子树（根节点为9）」。因为节点6和9都是叶子节点了，所以也返回啦。
文章插图
左子树（根节点为2）和右子树(根节点为7）都被翻转完后，这几个步骤就「归来」，即递归的归过程，翻转树的任务就完成了~