程序员必备的基本算法：递归详解( 四 ) 前言递归是一种非常重要的算法思想

一个子问题时间 = f（n-1）+f（n-2），也就是一个加法的操作，所以复杂度是「O(1)」；
问题个数 = 递归树节点的总数，递归树的总结点 = 2^n-1 ，所以是复杂度「O(2^n)」。

因此，青蛙跳阶，递归解法的时间复杂度 = O(1) * O(2^n) = O(2^n) ，就是指数级别的，爆炸增长的，「如果n比较大的话，超时很正常的了」。
回过头来，你仔细观察这颗递归树，你会发现存在「大量重复计算」，比如f（8）被计算了两次， f（7）被重复计算了3次...所以这个递归算法低效的原因，就是存在大量的重复计算！
「那么，怎么解决这个问题呢？」
既然存在大量重复计算，那么我们可以先把计算好的答案存下来，即造一个备忘录，等到下次需要的话，先去「备忘录」查一下，如果有，就直接取就好了，备忘录没有才再计算，那就可以省去重新重复计算的耗时啦！这就是「带备忘录的解法」
我们来看一下「带备忘录的递归解法」吧~
一般使用一个数组或者一个哈希map充当这个「备忘录」。
假设f(10)求解加上「备忘录」，我们再来画一下递归树：
「第一步」， f（10）= f(9) + f(8) ， f(9) 和f（8）都需要计算出来，然后再加到备忘录中，如下：

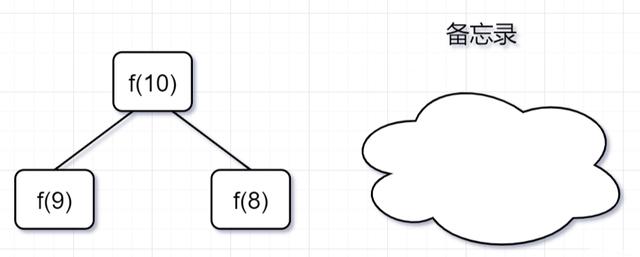文章插图
「第二步，」 f(9) = f（8）+ f（7）， f（8）= f（7）+ f(6), 因为 f(8) 已经在备忘录中啦，所以可以省掉， f(7),f（6）都需要计算出来，加到备忘录中~

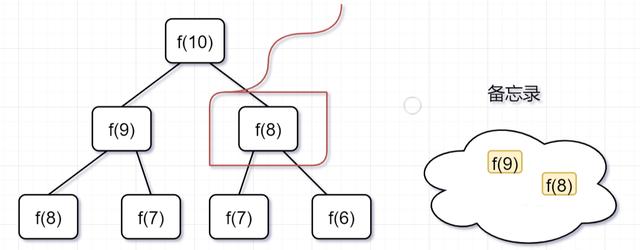文章插图
「第三步，」 f(8) = f（7）+ f(6),发现f(8) ， f(7),f（6）全部都在备忘录上了，所以都可以剪掉。

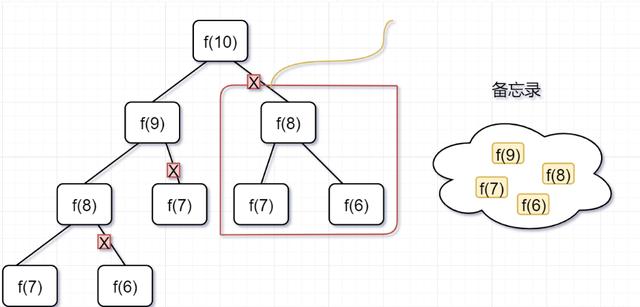文章插图
所以呢，用了备忘录递归算法，递归树变成光秃秃的树干咯，如下：

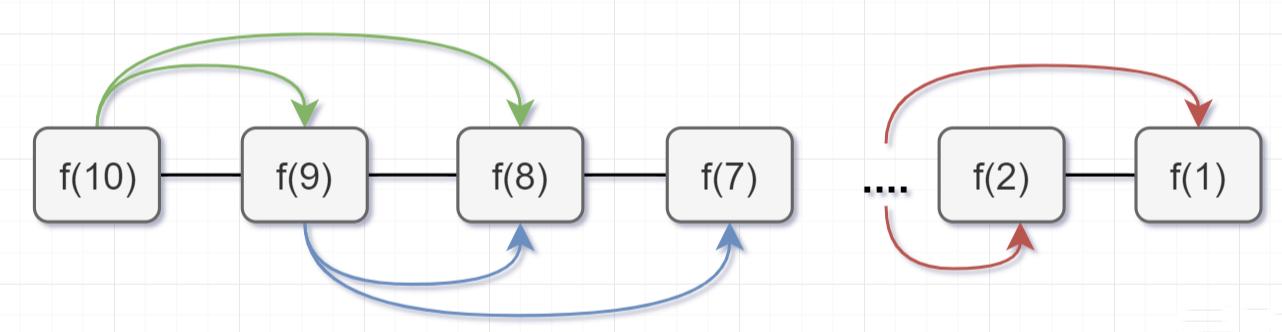文章插图
带「备忘录」的递归算法，子问题个数=树节点数=n ，解决一个子问题还是O(1),所以「带「备忘录」的递归算法的时间复杂度是O(n)」。接下来呢，我们用带「备忘录」的递归算法去撸代码，解决这个青蛙跳阶问题的超时问题咯~ ，代码如下：

public class Solution {//使用哈希map ， 充当备忘录的作用Map tempMap = new HashMap();public int numWays(int n) {// n = 0 也算1种if (n == 0) {return 1;}if (n <= 2) {return n;}//先判断有没计算过 ， 即看看备忘录有没有if (tempMap.containsKey(n)) {//备忘录有 ， 即计算过 ， 直接返回return tempMap.get(n);} else {// 备忘录没有 ， 即没有计算过 ， 执行递归计算,并且把结果保存到备忘录map中 ， 对1000000007取余（这个是leetcode题目规定的）tempMap.put(n, (numWays(n - 1) + numWays(n - 2)) % 1000000007);return tempMap.get(n);}}}

去leetcode提交一下，如图，稳了：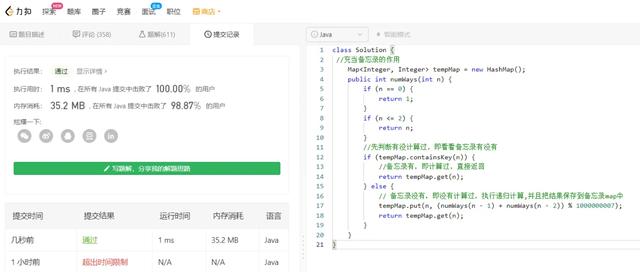

文章插图
来自：