时序数据异常检测做到这种段位，还怕什么告警风暴( 四 ) 作者介绍胡原、锦冬、俊峰

图8 监督学习在分类问题中的应用
监督学习整体思路[10]如上图8所示，其中(x1,y1),(x2,y2),…,(xn,yn)是训练数据集，学习系统由训练数据学习一个分类器P(Y∣X)或Y=f(X) ，分类系统通过学习到的分类器对新的输入实例xn+1进行分类，预测其输出的类别yn+1 。
2）异常注入
一般而言，在样本数据集中，正负样本比例如果极度不均衡（比如1:5 ，或者更悬殊），那么分类器分类时就会倾向于高比例的那一类样本（假如负样本占较大比例，则会表现为负样本Recall过高，正样本Recall低，而整体的Accuracy依然会有比较好的表现）。
在一个极度不均衡的样本集中，由于机器学习会对每个数据进行学习，那么多数数据样本带有的信息量就比少数样本信息量大，会对分类器学习过程中造成干扰，导致分类不准确。
在实际生产环境中，时序数据异常点是非常少见的， 99%以上的数据都是正常的。如果使用真实生产环境的数据进行样本标注，将会导致正负样本比例严重失衡，导致精召率无法满足要求。
为了解决基于监督学习的异常检测异常点过少的问题，本文设计一种针对周期型指标的自动异常注入算法，保证异常注入足够随机且包含各种异常场景。
时序数据的异常分为两种基本类型，异常上涨和异常下跌，如下图9（图中数据使用Curve[11]标注），通常异常会持续一段时间，然后逐步恢复，恢复过程或快或慢，影响异常两侧的值，称之为涟漪效应（Ripple Effect），类似石头落入水中，波纹扩散的情形。
受到该场景的启发，异常注入思路及步骤如下：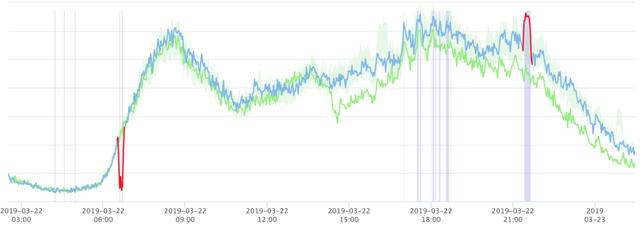
文章插图
图9 异常case中异常数据分布

给定一段时序值S ，确定注入的异常个数N ，将时序数据划分为N块；
在其中的一个区域X中，随机选定一个点Xi作为异常种子点；
设定异常点数目范围，基于此范围产生随机出异常点数n ，异常点随机分布在异常种子两侧，左侧和右侧的数目随机产生；
对于具体的异常点，根据其所在位置，选择该点邻域范围数据作为参考数据集m ，需要邻域在设定的范围内随机产生；
产生一个随机数，若为奇数，则为上涨，否则下跌。基于参考数据集m ，根据3Sigma原理，生成超出±3σ的数据作为异常值；
设定一个影响范围，在设定范围内随机产生影响的范围大小，左右两侧的影响范围也随机分配，同时随机产生异常衰减的方式，包括简单移动平均、加权移动平均、指数加权移动平均三种方式；
上述过程只涉及突增突降场景，而对于同时存在升降的场景，通过分别生成上涨和下跌的上述两个异常，然后叠加在一起即可。

通过上面的异常注入步骤，能比较好地模拟出周期型指标在生产环境中的各种异常场景。上述过程中各个步骤的数据都是随机产生，所以产生的异常案例各不相同，从而能为我们生产出足够多的异常样本。

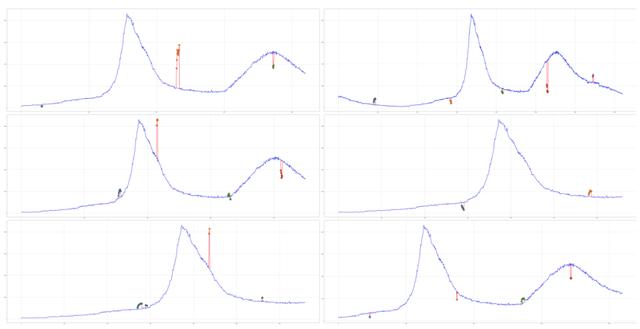
文章插图
图10 异常注入效果图
为了保证样本集的高准确性，我们对于注入异常后的指标数据还会进行标注，以去除部分注入的非异常数据。具体异常数据生成效果如图10所示，其中蓝色线为原始数据，红色线为注入的异常，可以看出注入异常与线上环境发生故障时相似，注入的异常随机性较大。
3）特征工程
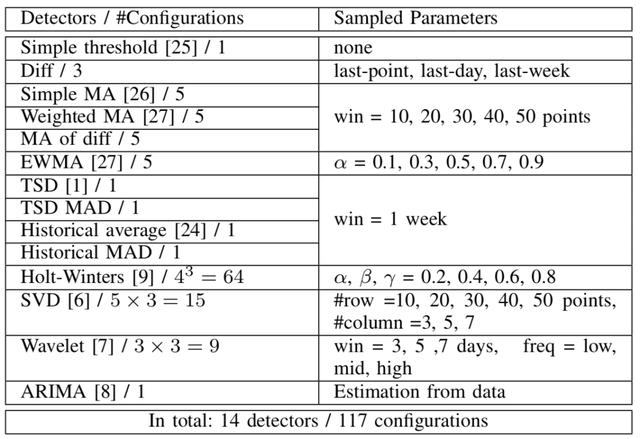
针对周期型指标，经标注产生样本数据集后，需要设计特征提取器进行特征提取， Opprentice中设计的几种特征提取器如图11所示：

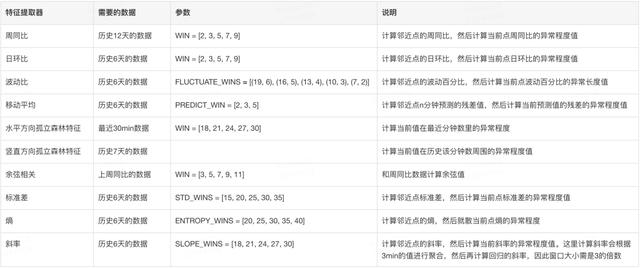
文章插图
图11 论文Opprentice特征提取器
上述特征主要是一些简单的检测器，包括如固定阈值、差分、移动平均、SVD分解等。 Metis将其分为三种特征：

一是统计特征，包括方差、均值、偏度等统计学特征；
二是拟合特征，包括如移动平均、指数加权移动平均等特征；
三是分类特征，包含一些自相关性、互相关性等特征。

参考上述提及的特征提取方法，本文设计了一套特征工程。区别于上述特征提取方法，本文对提取的结果用孤立森林进行了一层特征抽象，使得模型的泛化能力更强，所选择的特征及说明如下：

文章插图