图解：数据结构中的6种「树」，你心中有数吗？( 二 ) 数据结构这门课程是计算机相

没有父节点的节点称为根节点；

每一个非根节点有且只有一个父节点；

除了根节点外，每个子节点可以分为多个不相交的子树；

树里面没有环路，意思就是从一个节点出发，除非往返，否则不能回到起点。

二叉树有了前面「树」的基础铺垫，二叉树是一种特殊的树，还记的上面我们学过「节点的度」吗？二叉树中每个节点的度不大于 2，即它的每个节点最多只有两个分支，通常称二叉树节点的左右两个分支为左右子树。
二叉树是很多其他树型结构的基础结构，比如下面要讲的 AVL 树、二叉查找树，他们都是由二叉树增加一些约束条件进化而来。
三种遍历方式二叉树的遍历就是逐个访问二叉树节点的数据，常见的二叉树遍历方式有三种，分别是前中后序遍历，初学者分不清这几个顺序的差别。
「有个简单的记忆方式，这里的「前中后」都是对于根节点而言」。
先访问根节点后访问左右子树的遍历方式是前序遍历，先访问左右子树最后访问根节点的遍历方式是后序遍历，先访问左子树再访问根节点最后访问右子树的遍历方式是中序遍历，下面详细说明：

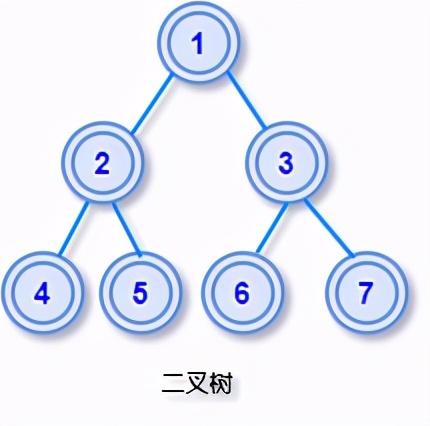
文章插图
前序遍历遍历顺序是根节点->左子树->右子树
遍历的得到的序列是：1 2 4 5 3 6 7
中序遍历遍历顺序是左子树->根节点->右子树
遍历的得到的序列是：4 2 5 1 6 3 7
后序遍历遍历顺序是左子树->右子树->根节点
遍历的得到的序列是：4 5 2 6 7 3 1
二叉查找树由于最基础的二叉树节点是无序的，想象一下如果在二叉树中查找一个数据，最坏情况可能要要遍历整个二叉树，这样的查找效率是非常低下的。
由于基础二叉树不利于数据的查找和插入，因此我们有必要对二叉树中的数据进行排序，所以就有了「二叉查找树」，可以说这种树是为了查找而生的二叉树，有时也称它为「二叉排序树」，都是同一种结构，只是换了个叫法。
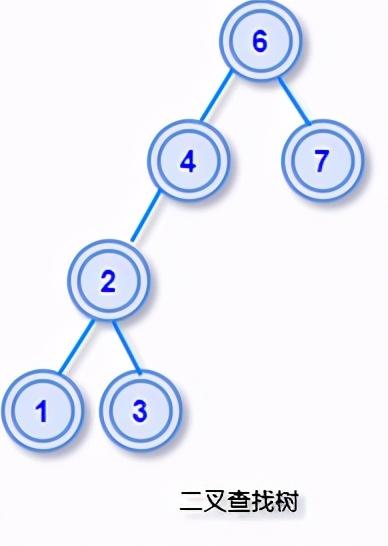
查找二叉树理解了也不难，简单来说就是二叉树上所有节点的，左子树上的节点都小于根节点，右子树上所有节点的值都大于根节点。

文章插图
这样的结构设计，使得查找目标节点非常方便，可以通过关键字和当前节点的对比，很快就能知道目标节点在该节点的左子树还是右子树上，方便在树中搜索目标节点。
如果对排序二叉树执行中序遍历，因为中序遍历的顺序是：左子树->根节点->右子树，最终可以得到一个节点值的有序列表。
举个栗子：对上图的排序二叉树执行中序遍历，我们可以得到一个有序序列：1 2 3 4 5 6 7
查询效率二叉查找树的查询复杂度取决于目标节点的深度，因此当节点的深度比较大时，最坏的查询效率是O(n) ，其中n是树中的节点个数。
实际应用中有很多改进版的二叉查找树，目的是尽可能使得每个节点的深度不要过深，从而提高查询效率。比如AVL树和红黑树，可以将最坏效率降低至O(log n) ，下面我们就来看下这两种改进的二叉树。
AVL树AVL 也叫平衡二叉查找树。 AVL 这个名字的由来，是它的两个发明者G. M. Adelson-Velsky 和 Evgenii Landis 的缩写， AVL最初是他们两人在1962 年的论文「An algorithm for the organization of information」中提出来一种数据结构。
定义AVL 树是一种平衡二叉查找树，二叉查找树我们已经知道，那平衡是什么意思呢？
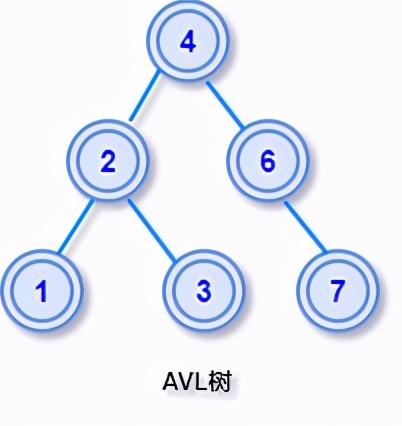
我们举个天平的例子，天平两端的重量要差不多才能平衡，否则就会出现向一边倾斜的情况。把这个概念迁移到二叉树中来，根节点看作是天平的中点，左子树的高度放在天平左边，右子树的高度放在天平右边，当左右子树的高度相差「不是特别多」，称为是平衡的二叉树。

文章插图
AVL树有更严格的定义：在二叉查找树中，任一节点对应的两棵子树的最大高度差为 1 ，这样的二叉查找树称为平衡二叉树。其中左右子树的高度差也有个专业的叫法：平衡因子。
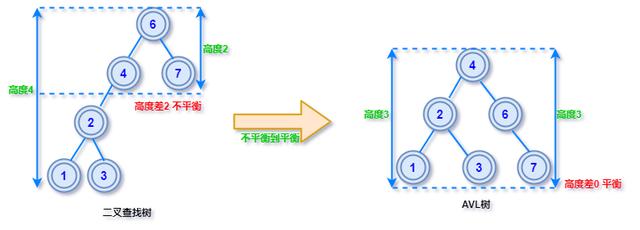
AVL树的旋转一旦由于插入或删除导致左右子树的高度差大于1 ，此时就需要旋转某些节点调整树高度，使其再次达到平衡状态，这个过程称为旋转再平衡。

文章插图