图解：数据结构中的6种「树」，你心中有数吗？( 三 ) 数据结构这门课程是计算机相

保持树平衡的目的是可以控制查找、插入和删除在平均和最坏情况下的时间复杂度都是O(log n) ，相比普通二叉树最坏情况的时间复杂度是 O(n)， AVL树把最坏情况的复杂度控制在可接受范围，非常合适对算法执行时间敏感类的应用。
B树B树是鲁道夫·拜尔（Rudolf Bayer）1972年在波音研究实验室（Boeing Research Labs）工作时发明的，关于B树名字的由来至今是个未解之谜，有人猜是Bayer的首字母，也有人说是波音实验室（Boeing Research Labs）的Boeing首字母缩写，虽然B树这个名字来源扑朔迷离，我们心里也没点 B 树，但不影响今天我们来学习它。
定义一个 m 阶的B树是一个有以下属性的树

每一个节点最多有 m 个子节点
每一个非叶子节点（除根节点）最少有 ?m/2? 个子节点， ?m/2?表示向上取整。
如果根节点不是叶子节点，那么它至少有两个子节点
有 k 个子节点的非叶子节点拥有 k ? 1 个键
所有的叶子节点都在同一层

如果之前不了解，相信第一眼看完定义肯定是蒙圈，不过多看几遍好好理解一下就好了，画个图例，对照着看看：

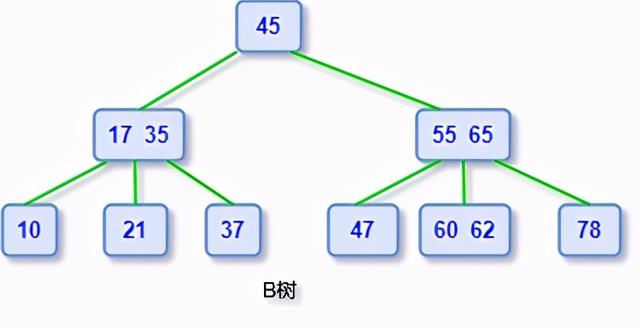文章插图
图3
特点

B树是所有节点的平衡因子均等于0的多路查找树（AVL树是平衡因子不大于 1 的二路查找树）。
B 树节点可以保存多个数据，使得 B 树可以不用像 AVL 树那样为了保持平衡频繁的旋转节点。
B树的多路的特性，降低了树的高度，所以B树相比于平衡二叉树显得矮胖很多。
B树非常适合保存在磁盘中的数据读取，因为每次读取都会有一次磁盘IO ，高度降低减少了磁盘IO的次数。

B树常用于实现数据库索引，典型的实现， MongoDB索引用B树实现， MySQL的Innodb 存储引擎用B+树存放索引。
说到B树不得不提起它的好兄弟B+树，不过这里不展开细说，只需知道， B+树是对B树的改进，数据都放在叶子节点，非叶子节点只存数据索引。
红黑树红黑树也是一种特殊的「二叉查找树」。
到目前为止我们学习的 AVL 树和即将学习的红黑树都是二叉查找树的变体，可见二叉查找树真的是非常重要基础二叉树，如果忘了它的定义可以先回头看看。
特点红黑树中每个结点都被标记了红黑属性，红黑树除了有普通的「二叉查找树」特性之外，还有以下的特征：

节点是红色或黑色。
根是黑色。
所有叶子都是黑色（叶子是NIL节点）。
每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

这些性质有兴趣可以自行研究，不过，现在你只需要知道，这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。

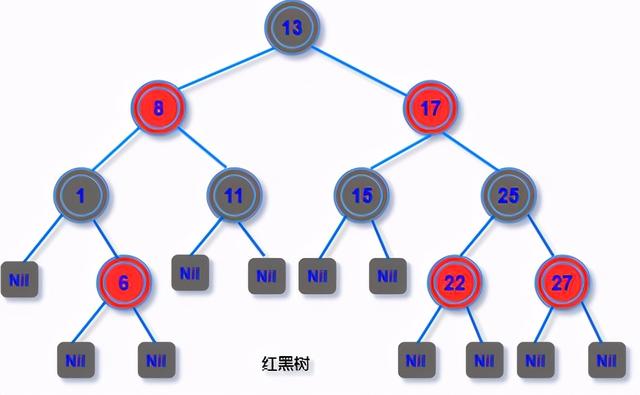文章插图
红黑树
而节点的路径长度决定着对节点的查询效率，这样我们确保了，最坏情况下的查找、插入、删除操作的时间复杂度不超过O(log n) ，并且有较高的插入和删除效率。
应用场景红黑树在实际应用中比较广泛，有很多已经落地的实践，比如学习C++的同学都知道会接触到 STL 标准库，而STL容器中的map、set、multiset、multimap 底层实现都是基于红黑树。
再比如， Linux内核中也有红黑树的实现， Linux系统在实现EXT3文件系统、虚拟内存管理系统，都有使用到红黑树这种数据结构。
Linux内核中的红黑树定义在内核文件如下的位置：

文章插图
如果找不到，可以 find / -name rbtree.h 搜索一下即可，有兴趣可以打开文件看下具体实现。
红黑树 VS 平衡二叉树（AVL树）

插入和删除操作，一般认为红黑树的删除和插入会比 AVL 树更快。因为，红黑树不像 AVL 树那样严格的要求平衡因子小于等于1 ，这就减少了为了达到平衡而进行的旋转操作次数，可以说是牺牲严格平衡性来换取更快的插入和删除时间。
红黑树不要求有不严格的平衡性控制，但是红黑树的特点，使得任何不平衡都会在三次旋转之内解决。而 AVL 树如果不平衡，并不会控制旋转操作次数，旋转直到平衡为止。
查找操作， AVL树的效率更高。因为 AVL 树设计比红黑树更加平衡，不会出现平衡因子超过 1 的情况，减少了树的平均搜索长度。
- 上一页
- 1
- 2
- 3
- 4
- 下一页