傻大方提示您本文标题是：《2018年延迟退休变化，养老金什么时候开始涨？》。来源是不朽的原函数。

2018年延迟退休变化，养老金什么时候开始涨？。养老金|变化|模态|命题|方阵|延迟退休---

事业单位人员违纪将影响养老金

已经退休的事业单位工作人员涉嫌违纪违法的，不再作出处分决定，但应当立案调查并按程序作出调查结论，明确其应受处分的种类。对于应当给予降低岗位等级或者撤职以上处分的，其养老保险等相应待遇按有关规定执行。

养老金|变化|模态|命题|方阵|延迟退休---傻大方小编总结的关键词

2018年延迟退休变化

目前人社部并没有公布具体执行政策及实施时间，从人社部对外公布的数据表来看，延迟退休将在4年之后才会开始"渐进式"的实施，那就意味着中国将在2022年首次实施延迟退休政策。但是这项政策实施的具体时间还要等国家人社部公告，大家不要轻易相信外界传言，在人社部出台正式的具体政策及方案实施时间之前，传言永远是传言。不可轻易相信！

养老金|变化|模态|命题|方阵|延迟退休---傻大方小编总结的关键词

判断推理之模态命题推理

一、模态命题定义及分类

2018年延迟退休变化，养老金什么时候开始涨？。养老金|变化|模态|命题|方阵|延迟退休---

模态判断是陈述事物情况的必然性或可能性的判断。在语言表达上，表示模态的词有：“可能”、“必然”等。

模态命题可分为两类。

第一类为可能命题，也叫或然命题，反映事物情况可能性的命题。又分为可能肯定和肯可能否定命题。如河流可能会干涸。今年冬天可能不会下雪。

第二类为必然命题。反映事物情况必然性的命题。又可分为必然肯定命题和必然否定命题。如台湾必然会回到祖国的怀抱。冬天到了，春天必然不会太遥远。

二、模态判断的逻辑结构

2018年延迟退休变化，养老金什么时候开始涨？。养老金|变化|模态|命题|方阵|延迟退休---

从结构来看，模态判断是由模态词和基础判断两部分组成。

模态词是模态判断中表示对象情况的必然性或可能性的概念。如：“如果”、“可能”、“也许”、“一定”等。模态词又分为两类，一类是必然模态词，另一类是可能模态词。必然模态词是表示对象情况的必然性概念，通常有“必然”、“一定”等。可能模态词是模态判断中表示对象情况的可能性的概念，通常有“可能”、 “大概”、“或许”等。

基础判断就是模态判断中除模态以外的判断。例如：张三可能是警官学校的学生。其中：张三是警官学校的学生。就是基础判断。

三、模态命题之间的关系

2018年延迟退休变化，养老金什么时候开始涨？。养老金|变化|模态|命题|方阵|延迟退休---

对于“必然P”、“不可能“P”、“可能P”和“可能非P”之间的相互关系，可以用对当逻辑方阵来表示(图1)，辅助记忆。

养老金|变化|模态|命题|方阵|延迟退休---傻大方小编总结的关键词

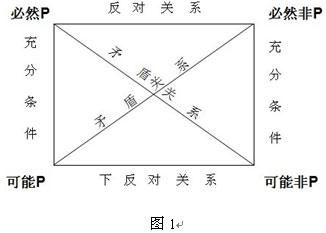
1、矛盾命题

(1)必然P→并非可能非P，并非必然P→可能非P;

(2)可能P→并非必然非P，并非可能P→必然非P;

(3)必然非P→并非可能P，并非必然非P→可能P;

(4)可能非P→并非必然P，并非可能非P→必然P;

2、反对及下反对命题

(1)必然P→并非必然非P，必然非P→并非必然P;

(2)并非可能P→可能非P，并非可能非P→可能P;

3、充分条件

(1)必然P→可能P;并非可能P→并非必然P;

(2)必然非P→可能非P，并非可能非P→并非必然非P。

巧解边端计数题

一、植树问题

2018年延迟退休变化，养老金什么时候开始涨？。养老金|变化|模态|命题|方阵|延迟退休---

单边线型植树公式：棵数=总长÷间隔+1;总长=(棵数-1)×间隔

单边环型植树公式：棵数=总长÷间隔;总长= 棵数×间隔

单边楼间植树(锯木、爬楼)公式：棵数=总长÷间隔-1;总长=(棵数+1)×间隔

特别提示：只要是直线型的路，不管有没有转弯，只要没有封闭就可以认为是线型植树问题;只要是封闭式的路，不管是什么形状的，我们都可以认为是环型植树问题。如果是双边植树，就在单边的基础上直接乘以2就可以了。

二、方阵问题

2018年延迟退休变化，养老金什么时候开始涨？。养老金|变化|模态|命题|方阵|延迟退休---

N阶实心方阵：总人数= (外圈人数÷4+1)2 ;最外圈为4N-4人;相邻两圈相差8人。

特别提示：给出的公式都是实心方阵适用的，也就是这类方阵中间是4人，如果题中给出的是中空方阵，那么就是意味着方阵的中间不是4人，因此在审题的时候大家务必要细心。

【精选例题】一根绳子对折三次后，从中剪断，共剪成( )段绳子。

A.9 B.6 C.5 D.3

【解析】A。本题是边端计数问题中的剪绳问题，从中间剪断只需要简一刀即可，套用公式，23×1+1=9，选择A选项。

片段阅读主旨题之并列结构

一、主旨概括题分类

2018年延迟退休变化，养老金什么时候开始涨？。养老金|变化|模态|命题|方阵|延迟退休---

1、找主旨句：主题句就是文段中的某句话。

2、总结主旨句：主题句不在文段中，而是要通过一定方法归纳出来的。(并列结构)

二、并列结构分类

2018年延迟退休变化，养老金什么时候开始涨？。养老金|变化|模态|命题|方阵|延迟退休---

1、宏观角度：“分—分”结构

例：“有关专家指出，物价涨幅过高不好，会影响经济的健康发展，影响人们的生活;物价水平过低，甚至出现负增长也不好，会影响企业的效益，进而影响社会就业和人们的收入。”

2、微观角度：由并列关联词引导的并列关系的一段文字。

例：“雨天，车身被蒙上一层土，这层土像细砂纸般包在车身上，一旦有摩擦，就如同用砂纸来磨车漆;此外，雨中含有各种有害物质，被泥沙吸住后，酸雨就很容易腐蚀车漆。”

这段文字就是由并列关联词“此外”构成的并列结构。

三、并列结构解题方法

2018年延迟退休变化，养老金什么时候开始涨？。养老金|变化|模态|命题|方阵|延迟退休---

方法一：从个性中找共性

“从个性中找共性”这是并列结构中囊括主题句较难的一种方法，更多是没有并列关联词引导的文段中使用较多，例如句式一致的分—分结构。它指的是，在并列的几句话中，找到每句话都有的共性，正确答案要能够找出涵盖的所有的共性。