从Bengio演讲发散开来：探讨逻辑推理与机器学习( 二 ) 机器之心分析师网络作者：仵冀颖编辑：

所有的逻辑都配备了一套与上述过程类似的推论方法。逻辑的这些原始内置方法的作用类似于编程语言中的标准库。有了这些方法，就可以将它们组合起来以得到更复杂的方法。
从教学的角度来看，从命题逻辑出发进行介绍是一个很好的起点。但是，对于实际中具有大量对象的领域建模来说，使用命题逻辑是很难处理的。例如，假设我们要写下数独游戏应该满足的约束条件。对于每个数 k ，每行 i 和列 j 都对应一个原子 A_ijk ，它代表「行 i 和列 k 包含数字 k」。这样，我们就可以在命题逻辑中快速写出数独的约束条件。例如，下图中的句子说明数字 5 应该出现在第一行中。
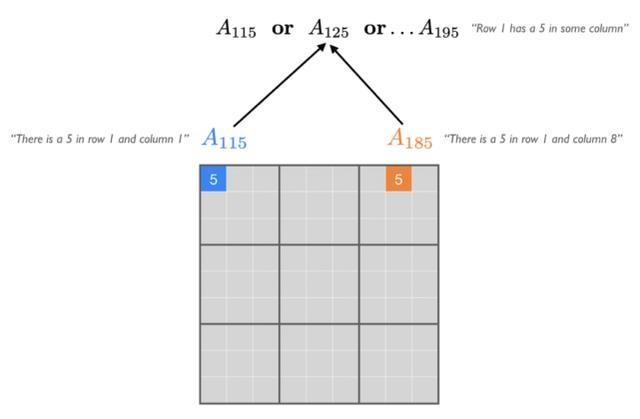文章插图
同样，我们也可以写下其他数字的其他约束条件。在我们的约束条件下，总共有 9^3=729 个原子。每一个原子可以是真或假，即表征总共 2 种可能的状态（远大于宇宙中物理原子的数量）。
一阶逻辑通过引入原子来改进命题逻辑，这些原子可以接受域中对象的参数。在一阶逻辑中将有一个原子来接受这些变量作为参数，而不是用一个原子 A_ijk 来表示 i、j 和 k 的每个组合。例如， A(1,3,5)表示第 1 行和第 3 列中有一个 5 。下图表示第 1 行中有一列的数字是 5 。
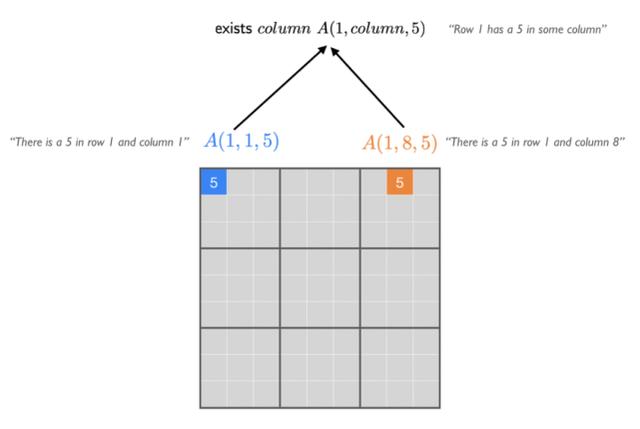文章插图
一阶逻辑是许多现代逻辑系统在研究和工业中应用的基础。许多其他逻辑系统建立并扩展了一阶逻辑（例如，二阶逻辑、三阶逻辑、高阶逻辑和模态逻辑）。每一种逻辑都增加了一个新的维度或特性，以便更容易对世界的某些方面进行建模。例如，被称为时态逻辑的逻辑被用来对时间和变化进行建模。
1.2 AI/ML 中的逻辑
1.2.1 科学中的自动发现
逻辑学最成功的应用之一是在科学领域中表示结构化的科学知识。 2007 年，威尔士和英格兰的一个小组创建了一个名为 Adam（自动发现和分析机器）的系统 [1] 。 Adam 可以自动形成科学假设，进行实验来检验假设并记录实验结果。这是第一个自动系统，用来发现各类的科学信息。 Adam 成功地应用于确定酵母中的一些基因。在这个系统中，假设、实验结果和结论都以逻辑的形式表达出来。
1.2.2 归纳程序设计
归纳程序设计的目标是学习给定一组输入和输出示例的计算机程序。归纳程序设计处理的是可以从这些例子中学习的生成系统。这种系统通常是用逻辑来表述的。最先进的归纳程序设计系统可以从几个例子中学习复杂的递归程序。目前，归纳程序设计方法已经被用来学习数据清理和转换程序任务[2] 。
1.2.3 数学推理自动化
上面的数独例子说明了一阶逻辑比命题逻辑更具表现力。不过，我们能用它来模拟的东西有限制吗？实际上，单是一阶逻辑就相当强大，它强大到可以模拟几乎所有的古典数学。在标准数学的概念下工作，使用一阶逻辑可以陈述你想要证明的任何目标（一个猜想），并能让机器自动检查你的工作（数学证明）。这种方法就是直接使用数学的推理自动化。
1.2.4 计算机系统（包括机器学习系统）的验证
在数学之外，以一阶逻辑和类似系统为基础的逻辑被用于验证计算机系统。这种选择被称为正式验证（Formal Verification）。在正式的验证中，有一个计算机系统 S 和一个属性 P ，用户必须用一种相对严格的方式来验证这个属性是有效的。例如，用于验证硬件和软件系统的工业强度系统 ACL2 () 。
1.2.5 类似逻辑系统与机器学习模型
随着越来越多的应用程序和领域使用机器学习模型，仍有一些场景需要使用类似逻辑系统和机器学习模型。例如，许多欺诈检测系统使用一个或多个机器学习模型以及大量手工编制的规则，而这些规则是非常必要的。在欺诈检测领域，这些规则可能会捕获新的和不断发展的欺诈模式，而针对这些模式可能并没有足够的数据来训练得到新的模型[3] 。