从Bengio演讲发散开来：探讨逻辑推理与机器学习( 四 ) 机器之心分析师网络作者：仵冀颖编辑：

本文提出的诱因学习（ABL）试图通过逻辑诱因和一致性优化来解决这些挑战。给定一个与最终输出相关联的训练样本，逻辑推理可以对缺失的信息（例如，示例中的候选原始事实，或能够完成背景知识的逻辑子句）进行推测，以建立从样本到最终输出的一致性证明。然后，分别用导出的原始事实和逻辑子句训练机器学习模型，并将其作为符号知识存储。一致性优化被用来最大化推测与背景知识之间的一致性。为了解决这个高度复杂的问题，作者将其转换为一个任务，即搜索函数，猜测可能错误的原始事实。
由于收集玛雅象形文字数据是非常困难的，作者设计了一个类似的任务——「手写方程解谜」用于实验。该任务具体为学习图像识别（感知）和数学运算计算方程（推理）。实验结果表明， ABL 比最先进的深度学习模型具有更好的泛化能力，并且能够以一种互利的方式利用机器学习和推理。作者在一个可视化 n 皇后任务上的实验进一步证明， ABL 框架是非常灵活的，可以利用约束逻辑编程等经典符号 AI 系统来提高机器学习的性能。
2.1.2 方法简介
诱因性学习的任务可以形式化的表示如下。诱因性学习的输入由一组标记的关于目标概念 C 和领域知识库 B 的训练数据组成 D = {, . . . ,}。目标概念 C 是在一组原始概念符号 P=之间的未知关系下定义的。其中每个 pk 都是 B 中定义的符号。 ABL 的目标是输出一个假设模型 H=p∪?C：
p 是从特征空间到原始符号的映射，即它是一个传统机器学习的感知模型；
?C 是一组用 B 定义目标概念 C 的一阶逻辑子句，称为知识模型。
假设模型应满足：
(1)
其中，符号｜= 表示逻辑暗含（logical entailment）。从公式（1）可以看出，诱因性学习的主要挑战是感知模型 p 和知识模型?C 之间的相互依赖关系：1）需要依赖于感知结果 p(x)来学习 ?C ， p(x)为 x 中原始概念的集合。 2）为了得到 p ，需要得到用于训练的基本真值标签 p(x) ， p(x)可以从 B∪?C 和 y 的逻辑推导出来。当机器学习模型训练不足时，感知到的原始符号 p(x)极有可能不正确，因此作者将其命名为伪基元（pseudo-groundings）或伪标签（pseudo-labels）。因此，基于公式（1）的 ?C 推理是不一致的，当知识模型?C 不准确时，逻辑推导出的伪标签 p(x)也可能出错，从而影响了 p 的训练，而无论哪种方式都会中断学习过程。
ABL 试图通过将机器学习与诱因性逻辑推理模块相连接，并通过一致性优化将它们的内部机制融合起来，从而解决这些挑战。 ABL 的完整框架见图 3 。其中，机器学习（Machine Learning）用于学习感知模型 p：给定一个输入实例 x ， p 可以预测伪标签 p(x)作为 x 中可能的原始概念的真值。当伪标签包含错误时，需要重新训练感知模型，此时，所使用的标签是逻辑诱因返回的修正后的伪标签 r(x) 。逻辑诱因（Logical abduction）是诱因推理的逻辑形式化表示。给定以一阶逻辑子句形式表述的观测事实和背景知识，逻辑推理将对观测事实的可能性解释扩展为基本假设。
文章插图
图 3. ABL 完整框架
逻辑程序（Logic Programming）中的一个声明性框架将上述的过程形式化，称为诱因性逻辑程序（Abductive Logic Programming ， ALP）[8] 。形式上，诱因性逻辑程序（abductive logic program）可以定义如下：
定义 1：诱因性逻辑程序是一个三元组 (B,A,IC) ，其中 B 是背景知识， A 是一组可扩展谓词， IC 是完整性约束。给定一些观测事实 O ，程序输出为一组 A 的真值推理结果? ，如：
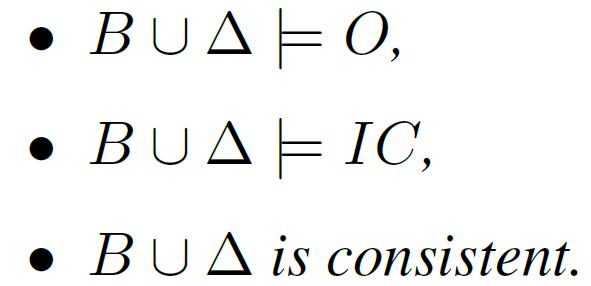文章插图