从Bengio演讲发散开来：探讨逻辑推理与机器学习( 九 ) 机器之心分析师网络作者：仵冀颖编辑：

（8）
【通过 SDP 的反向传播】
得到 δl/δV_O 后，通过 SDP 推导出解 δl/δS：
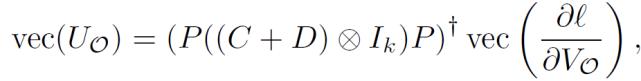文章插图
（9）
【从松弛结果到原始输入】
最后，使用梯度 δl/δV_I 通过输入松弛过程推导梯度 δl/δZ_x：
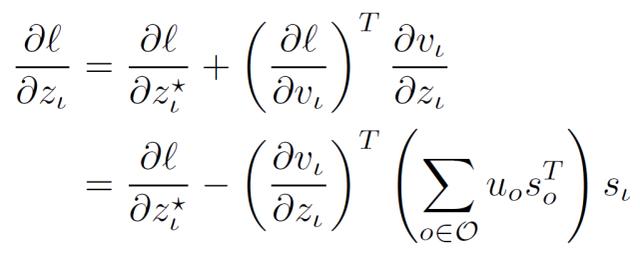文章插图
（12）
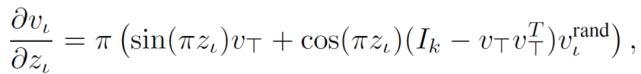文章插图
（13）
2.2.2 实验分析
在实验部分，作者证明了 SATNet 可以集成到深度神经网络架构中进行端到端的训练。作者选择了一个可视化数独问题进行实验：即，给定一个用 MNIST 数字构造的数独板的图像表示（而不是一个热编码或其他逻辑表示），深度神经网络必须输出与之相关联的数独问题的逻辑解。
图 3 给出了一个输入示例。使用经典的深度神经网络体系架构无法解决这个问题，因为解决这个问题要求能在不将问题的逻辑结构硬编码为中间逻辑层的前提下组合多个神经网络层。本文的神经网络使用了一个连接到 SATNet layer 的卷积网络结构。具体来说，将一个用于数字分类的卷积层（使用 LeNet 架构）应用到数独输入的每个单元。然后，将该卷积层的每个单元概率输出作为逻辑输入输入到 SATNet layer 。这个 SATNet layer 采用与前面描述相同的架构和训练参数。整个模型经过端到端的训练以最小化交叉熵损失，并通过 Adam 进行优化， SATNet layer 的学习率为 2x10^(?3) ，卷积层的学习率为 10^(?5) 。
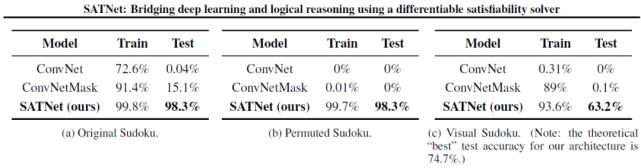
作者将本文的方法与结合了两组卷积层的卷积神经网络进行了比较，表 1 给出了实验结果。将这些结果与 74.7% 的理论「最佳」测试精度结合起来，这解释了特定的卷积结构的数独数字分类准确率。假设板子上 81 个填充单元中平均有 36.2 个单元（如测试集中）和一个 MNIST 模型，测试准确率为 99.2% ，期望一个完美的数独解算器输出正确解的时间为 74.7% 。（=0.99236.2）。在 100 个周期中，本文模型在测试时能够正确求解出 63.2% 的棋盘，达到理论「最佳」的 85% 。本文方法在端到端求解可视化数独板方面表现出很强的性能。另一方面，基线卷积网络在 100 个周期的过程中对训练损失的改善微乎其微。因此，本文的 SATNet 架构能够直接从图形输入中进行端到端的「游戏规则」学习，这种学习方式在以前的架构中是不可能的。
文章插图
表 1. 9x 9 个数独实验的结果，将 SATNet 模型与一个普通的卷积神经网络（ConvNet）以及一个接收二进制掩码指示需要学习哪些位的网络（ConvNetMask）进行比较。
2.2.3 文章小结
这项工作涵盖了深度学习和逻辑推理的知识。目前，一些研究人员已经提出了许多「可微逻辑推理」系统，但大多数系统仍然需要预先手工参与确定的逻辑规则和真值基础，因此这些方法在某种程度上限制了它们以真正的端到端方式进行处理的能力。本文将强大而通用的逻辑处理器（如 MAXSAT 解算器）封装在一个可微框架内，该解算器可以应用在更大的深度学习框架内进行「隐式」逻辑推理。作者认为， SATNet 为整合符号推理和深度学习（人工智能的长期目标）迈出了一步。
3. 应用数据库介绍
3.1 LogiQA: A Challenge Dataset for Machine Reading Comprehension with Logical Reasoning [7]
本文是 IJCAI 2020 中的一篇录用文章，是由来自复旦大学和西湖大学的研究人员共同完成的，主要研究目的是构建一个用于测试逻辑推理能力的阅读理解数据库 LogiQA 。与上一节介绍的模型方法不同，本文主要介绍的是应用于逻辑推理和机器学习任务的数据库的构建，以及结合具体的 NLP 任务介绍将逻辑推理和机器学习方法相结合的作用和意义。