从Bengio演讲发散开来：探讨逻辑推理与机器学习( 七 ) 机器之心分析师网络作者：仵冀颖编辑：

2.2 SATNet: Bridging deep learning and logical reasoning using a differentiable satisfiability solver [6]
文章插图
本文是 ICML 2019 中获得最佳论文提名的一篇文章。由于上一篇文章《Bridging Machine Learning and Logical Reasoning by Abductive Learning》在 2018 年已经在 arXiv 上进行了发布，所以本文有参考引用并对比分析了与上一篇文章的不同。上一篇文章所介绍的方法是从现有的一组已知关系中创建一个模块（逻辑诱因模块），以便深层网络能够学习到这些关系的参数。因此，该方法需要植入变量之间关系的先验信息。本文所提出的方法则是端到端学习这些关系及其相关参数，即，本文引入了一个可微（平滑）最大可满足性（maximum satisfiability ， MAXSAT）求解器，并将其直接集成到深度学习系统的回路中，而不是作为一个单独的分离模块所考虑。该求解器基于快速坐标下降法来解决与 MAXSAT 问题相关的半定程序（semidefinite program ， SDP）。具体见第一篇文章中的「图 3. ABL 完整框架」。 ABL 框架包括了两个独立的模块「Machine Learning」和「Logical Abduction」。逻辑诱因性分析是一个与机器学习 ML 完全分离的单独模块。而在这篇文章中，作者考虑，不将逻辑推理和 ML/DL 完全分离开，而是将逻辑推理作为深度学习系统完整回路中的一个部分，实现端到端的学习。
2.2.1 方法介绍
MAXSAT 问题是著名的可满足性（satisfiability ， SAT）问题的优化模拟，其目标是使满足的子句数最大化。作者提出了一个可微的平滑的近似 MAXSAT 解算器，可以集成到目前的深度学习网络体系结构中。该解算器使用快速坐标下降法来求解 MAXSAT 的 SDP 松弛。考虑一个包含 n 个变量和 m 子句的 MAXSAT 实例。令 v 表示问题变量的二进制赋值， v_i 是变量 i 的真值，定义 s_i ，其中 s_ij 表述子句 j 中 v_i 的符号。 MAXSAT 问题定义为：
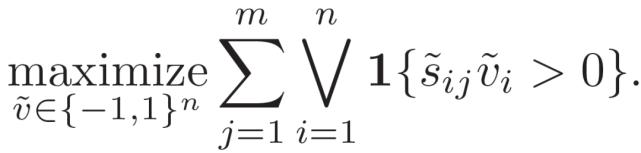文章插图
（1）
为了形成（1）的半定松弛约束，作者首先将离散变量 v_i 松弛为相关的连续变量且满足 ||v_i||=1 ，相对于某个「真值方向」v_T 满足 ||v_T||=1 。此外，定义一个对应于 v_T 的系数 s_T 。 MAXSAT 的 SDP 松弛为：
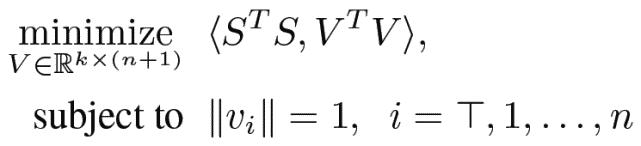文章插图
（2）
这个问题是 MIN-UNSAT 的一个低秩（但非凸）公式，它等价于 MAXSAT 。可以将这个公式重写为一个 SDP ，并且已经由研究人员证明给定 k>sqrt(2n)的情况下，该式可以恢复最优 SDP 解。尽管它是非凸的，可以通过坐标下降来优化地解决公式（2）。特别是，依赖于 v_i 的客观条件表示为：
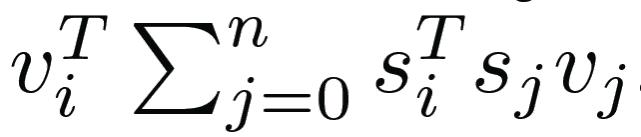文章插图
其中 s_i 是 S 的第 i 列向量。根据 ||v_i||=1 的约束条件，最小化 v_i 的值以得到坐标下降更新：
这些更新可证明能够收敛到 SDP(2)（即公式（2）对应的 SDP）的全局最优不动点。
使用 MAXSAT SDP 松弛和相关的坐标下降更新，作者创建了一个用于可满足性求解的深度网络层（SATNet）。令 I 表示已知赋值的 MAXSAT 变量的指数， O≡\I 对应于未知赋值的变量的指数。 SATNet Layer 允许以概率或二进制的形式输入 z_l∈[0,1] ， l∈I ，然后输出未知变量 z_o∈[0,1] ， o∈O 的赋值，这些未知变量具有类似的概率值或二进制值。令 Z_I 和 Z_O 分别表示全部的输入和输出任务。
通过 SDP(2)从输入 Z_I 生成输出 Z_O ， SATNet Layer 的权重对应于 SDP 的低秩系数矩阵 S 。完整的前向传递过程如图 1 所示，具体的层初始化和前向传递的步骤描述见算法 1 。