视觉|曼德尔球，分形几何中最伟大的突破之一，一场视觉盛宴( 二 ) 突破|视觉|几何|盛宴

该定理指出，如果二次形式在代数的非零部分将同态定义为正实数，那么代数必须与实数、复数、四元数或八元数同构。
上面简单的翻译为：对于我们的数字系统有某些操作（乘法/除法），他们必须在四个数学空间中的一个：实数（1D），复数（2D），四元数（4D）和八元数（8D）。
因此，基于这个理论，一个名叫艾伦·诺顿的人试图用四元数（4D）系统找到3D曼德尔布罗特等价。他的论文（发表于1982年）展示了通过展示4D空间的3D“切片”而完全实现的四元数朱莉娅集，这里有一个四元数朱莉娅分形的例子：
自然地，为了使一个四维物体形象化，你必须进行某种形式的维度缩减。最常见的方法是制作一个三维横截面，只需将四个元素中的一个保持在一个固定的值。不幸的是，虽然上面设置的四维朱莉娅集确实很吸引人，但在搜索四维曼德尔布罗特时，将四个分量中的一个保持在一个固定的值会造成二阶问题。通过强制元素保持固定，任何曼德尔布罗特创建的四元数都会自动在至少一个轴上对称：

文章插图
曼德尔球：分形几何最伟大的突破之一，视觉盛宴
在接下来的20年里，几乎没有什么表现。因此，对3D曼德尔布罗特集合的搜索直到2007年才有进展，当时一位名叫丹尼尔·怀特的业余数学家在参考体系中提出了一个深刻的转变。
怀特的洞察力，他的贡献，是从几何学上解释了曼德尔布罗特的定义——这使得在3D中工作更加实用。他没有像在2D曼德尔布罗特中那样绕着圆旋转，而是在三维球坐标（x，y，z）中绕着φ和θ旋转。
回想一下，曼德尔布罗特集强调了转义行为，即从变化复杂常量开始并遍历Z^2 + C。怀特的目的是复制这种几何的边界—极限关系。与曼德尔布罗特一样，在概念上，怀特设想将一个超级复杂的点（Z）平方以得到一个新的点，然后添加剩下的常数（C）。实际上，它有点复杂，因为平方增加了量级或到新点的距离；然而，在加C之前这个新点的方向是什么？
下面，我们将提供一种视觉效果，希望能帮助你直观地理解怀特的方法。之后，我们将逐步遍历上面代码的逻辑。我们试图在函数Z中拟合一组超复数 Z2 + C。从第一原理出发，让我们画出一个3D平面并随机选择一个点（x，y，z）：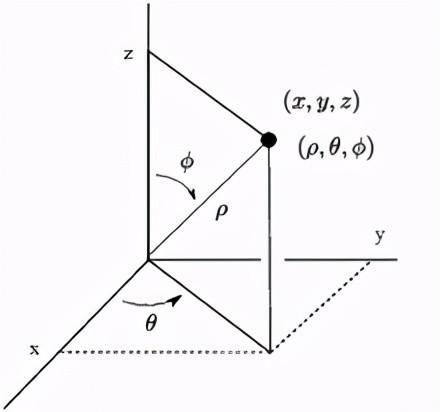

文章插图
double r = sqrt (x*x + y*y + z*z);double yAng = atan2 (sqrt(x*x + y*y), z);doubnt zAng = atan2 (y , x);
在(r)上方的起始线，就是3D中的距离公式。在分形世界中，这是原始公式Z的第一步。另一种看待这个的方法是r是向量的大小，它是旧点和新点之间的距离。然而，如上所述，这使我们缺乏方向——我们不知道这个新点在什么方向上。