领域|强化学习算法DeepCube，机器自行解决复杂魔方问题( 五 ) 自行解决|rl|强化|机器|算法

白色在顶部，绿色在左面，红色在前面；
绿色在顶部，红色在左面，白色在前面；
红色在顶部，白色在左面，绿色在前面；
因此，为精确表示角块的位置和方向，我们得到8×3=24种不同的组合。
至于12个侧面块，由于它们只有两个贴面，因此只能有两个方向。也得到24种组合，只不过是通过12×2=24计算得到的。最后，我们要跟踪20个立方块，8个角块和12个侧边块，每个立方块有24个可能的位置。
独热编码是指当前对象的位置为1且其他位置为0，该编码可以输入神经网络进行处理。因此，本文中状态的最终表示形式为20×24的张量。
考虑到冗余情况，这种表示方式非常接近总状态空间，其可能的组合数量为242?≈4.02×102?。虽然它仍远大于魔方的状态空间，但是这种方式要比比对每个贴面的所有颜色进行编码要好得多。冗余得原因是魔方旋转自身得属性，如不可能只旋转一个角块或是一个侧边块，每次旋转总是会转一个面。
好了，数学知识就介绍这么多，如果你想了解更多，推荐Alexander Frey和David Singmaster撰写的著作“Handbook of Cubic Math”。
细心的读者可能会注意到，这样的魔方状态的张量表示有一个重大缺点：内存效率低下。实际上，如果将状态表示为20×24的浮点张量，我们浪费了4×20×24=1920字节的内存，考虑到在训练过程中需要表示数千种状态，这会导致数百万字节内存的损耗。为了克服这个问题，在本文的实现中，我使用两种表示形式：一种是张量，用做神经网络输入；另一种是更紧凑的表示形式，以便更长久地存储不同的状态。我们将这种紧凑状态保存为一系列列表，根据角块和侧边面的排列及其方向进行编码。这种表示方式不仅具有更高的内存效率（160字节），而且使魔方的转换也更加方便。
更多细节参见该模块，紧凑状态见函数namedtuple，神经网络张量表示见函数encode_inplace。
训练过程
现在我们已经知道了三阶魔方的状态是如何以20×24张量编码的，下面我会介绍本文使用的神经网络结构及其训练方法。
神经网络结构
下图是神经网络结构（取自原论文）：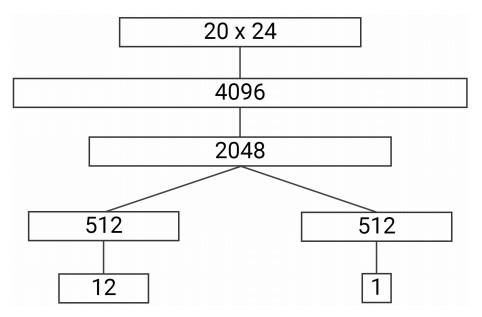

文章插图
该神经网络将魔方状态的20×24张量表示作为输入，并产生两个输出：
策略。由12个数字组成，表示行动的概率分布；
值。使用一个标量表示对状态的评估，具体含义见下文。
在输入和输出之间，神经网络由若干ELU激活函数的全连接层。在我的代码实现中，网络结构与此处并无差异，详见此处。
训练
可以看到，网络非常简单：策略告诉我们对当前状态进行何种转换，值用于评价状态的好坏程度。那么，最大的问题就是：如何训练网络？