模型|重点！11个重要的机器学习模型评估指标( 三 ) 全文共8139字

以阈值为0.5为例（参考混淆矩阵）。这是混淆矩阵：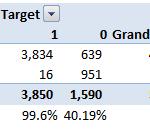
文章插图
如你所见，此时敏感度为99.6％，（1-特异性）大约为60％。该坐标在ROC曲线中成为点。为了将该曲线表达成数值，就要计算该曲线下的面积( AUC ) 。
注意，整个正方形的面积是1 * 1 = 1 。因此， AUC本身就是曲线下的比值和总面积。对于那个案例，得到AUC ROC的值为96.4％。以下是一些拇指规则( thumb rules )：
· 0.90-1=优秀(A）
· 0.80-0.90 =良好(B)
· 0.70-0.80 =一般(C)
· 0.60-0.70 =差(D)
· 0.50-0.60 =失败(F)
可以看出，目前的模型属于优秀范围。但也可能只是过度拟合。这种情况下，验证显得迫在眉睫了。
以下几点需注意：
1.对于作为类输出的模型，将在ROC图中用单个点表示。
2.这些模型无法相互比较，因为需要在单个指标基础上进行判断而不是多个指标。例如，具有参数（0.2,0.8）的模型和具有参数（0.8,0.2）的模型可以来自相同的模型，因此不应直接比较这些指标。
3.在概率模型的情况下，有幸能得到一个AUC-ROC的单个数字。但是，仍然需要查看整个曲线去做最终决定。又可能是一个模型在某些范围中性能更好，其他的在别的范围中更好。
使用ROC的优点
为什么要使用ROC而不是升力曲线等指标？
升力取决于人口的总响应率。因此，如果人口的响应率发生变化，同一模型将带来不同的升力图。解决这种问题的方案可以是真正的升力图（在每个十分位数处找到升力值和完美模型升力值的比率）。但这种比例很少对企业有价值。
另一方面， ROC曲线几乎与响应率无关。这是因为它有两个来自混淆矩阵柱状计算中的轴。在响应率变化的情况下， x轴和y轴的分子和分母也会有相应的改变。
文章插图
6. 对数损失
确定模型性能时AUC-ROC会考虑预测概率。然而， AUC ROC存在一个问题，就是只考虑概率的顺序，因此忽略了模型对更可能是正样本预测更高概率的能力。这种情况下，可以采取对数损失，它只是每个案例修正预测概率的对数的负平均值。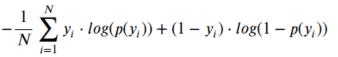
文章插图
· p( yi )是正类预测概率
· 1-p( yi )是负类预测概率
· yi = 1表示正类， 0表示负类（实际值）
随机计算几个值的对数损失，得出上述数学函数的要点：
Logloss（1,0.1）= 2.303
Logloss（1,0.5）= 0.693
Logloss（1,0.9）= 0.105
如果绘制这种关系，曲线图如下：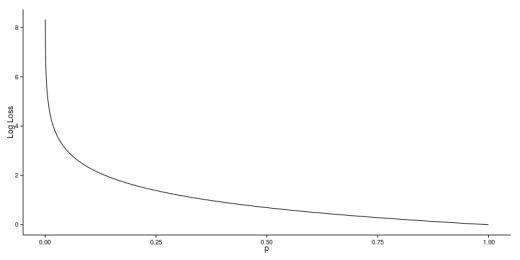
文章插图
从斜率向右下方逐渐平缓可以明显看出，随着预测概率的提高，对数损失值逐渐下降。不过反方向移动时，对数损失快速增加而预测概率趋近于0 。
因此，降低对数损失，对模型更好。但是，对于好的对数损失没有绝对的衡量标准，它取决于用例或者应用程序。
虽然AUC是根据具有不同决策阈值的二进制分类计算的，但对数损失实际上考虑了分类的“确定性” 。
文章插图
7. 基尼系数
基尼系数有时用于分类问题。基尼系数可由AUC ROC数直接导出。基尼只是ROC曲线和diagnol线之间的面积与上述三角形的面积之比。下面是使用公式：
Gini = 2*AUC – 1
基尼系数高于60％，模型就很好。对于目前的情况而言，基尼系数的值为92.7％。
文章插图
8. Concordant – Discordant ratio
对于任何分类预测问题，这也是最重要的指标之一。想要理解这个，先假设有3名学生今年有可能通过。以下是预测：
A – 0.9
B – 0.5
C – 0.3
现在想象一下。如果从这三个学生中挑两对，会有多少对？将有3种组合：AB、BC和CA 。现在，年底结束后， A和C通过了，而B没有。不行，选择所有配对，找到一个responder和其他non-responder 。这样的配对有多少？
有两对：AB和BC 。现在对于2对中的每一对，一致对( concordant pair )是responder的概率高于non-responder的。而不一致的对( discordant pair )虽情况相反但也是如此。如果两个概率相等，就称之为相当的。现在来看看案例中发生了什么：