如果说费米子是组成大楼的的砖头,那么玻色子就是水泥!
傻大方提示您本文标题是:《如果说费米子是组成大楼的的砖头,那么玻色子就是水泥!》。来源是灵遁者国学智慧。
如果说费米子是组成大楼的的砖头,那么玻色子就是水泥!。砖头|大楼|费米子|费米|狄拉克---
导读:本章摘自独立学者灵遁者量子力学科普书籍《见微知著》。此文旨在帮助大家认识我们身处的世界。世界是确定的,但世界的确定性不是我们能把我的。
接着我们来说说这位天才的其中之一费米—狄拉克统计理论。之所以叫费米—狄拉克统计。是因为费米和狄拉克分别独立的发展了这个理论。所以以他们两个人的名字命名。
费米-狄拉克统计
如果说费米子是组成大楼的的砖头,那么玻色子就是水泥!。砖头|大楼|费米子|费米|狄拉克---
,有时也简称费米统计如果说费米子是组成大楼的的砖头,那么玻色子就是水泥!。砖头|大楼|费米子|费米|狄拉克---
、FD统计如果说费米子是组成大楼的的砖头,那么玻色子就是水泥!。砖头|大楼|费米子|费米|狄拉克---
,在统计力学中用来描述由大量满足泡利不相容原理的费米子组成的系统中,粒子处在不同量子态上的统计规律。这个统计规律的命名来源于恩里科·费米和保罗·狄拉克,他们分别独立地发现了这一统计规律。不过费米在数据定义比狄拉克稍早。
砖头|大楼|费米子|费米|狄拉克---傻大方小编总结的关键词

费米–狄拉克统计的适用对象是,热平衡时自旋量子数为半奇数的粒子。除此之外,应用此统计规律的前提是——系统中各粒子之间的相互作用可以忽略不计。这样,就可以用粒子在不同定态的分布状况来描述大量微观粒子组成的宏观系统。
不同的粒子分处于不同的能态上,这一特点对系统许多性质会产生影响。费米–狄拉克统计适用于自旋量子数为半奇数的粒子,这些粒子也被称为费米子。由于电子的自旋量子数为1/2,因此它是费米–狄拉克统计最普遍的应用对象。费米–狄拉克统计是统计力学的重要组成部分,它利用了量子力学的一些原理。
砖头|大楼|费米子|费米|狄拉克---傻大方小编总结的关键词

根据量子力学,费米子为自旋为半奇数的粒子,其本征波函数反对称,在费米子的某一个能级上,最多只能容纳一个粒子。因而符合费米–狄拉克统计分布的粒子,当他们处于某一分布时(“某一分布”指这样一种状态:即在能量为
{\displaystyle \left\{\epsilon _{j}\right\}}的能级上同时有{\displaystyle n_{j}}
个粒子存在着,不难想象,当从宏观观察体系能量一定的时候,从微观角度观察体系可能有很多种不同的分布状态,而且在这些不同的分布状态中,总有一些状态出现的几率特别的大,而其中出现几率最大的分布状态被称为最可几分布)时,体系总状态数为:
砖头|大楼|费米子|费米|狄拉克---傻大方小编总结的关键词

1926年发现费米–狄拉克统计之前,要理解电子的某些性质较为困难。例如,在常温下,未施加电流的金属内部的热容比施加电流的金属少了大约100倍。此外,在常温下给金属施加一强电场,将造成场致电子发射(Field electron emission)现象,从而产生电流流经金属。研究发现,这个电流与温度几乎无关。当时的理论难以解释这个现象。
当时,由于人们主要根据的是经典静电学理论,因此在诸如金属电子理论等方面遇到的困难,无法得到令人满意的解答。他们认为,金属中所有电子都是等效的。也就是说,金属中的每个电子都以相同的程度对金属的热量做出贡献(这个量是波尔兹曼常数的一次项)。上述问题一直困扰着科学家,直到费米–狄拉克统计的发现,才得到较好地解释。
砖头|大楼|费米子|费米|狄拉克---傻大方小编总结的关键词

前面的章节叙述了给定费米子系统在不同量子态上的分布,一个量子态上最多只能具有一个费米子。利用费米–狄拉克统计,还可以获得费米子系统不同能量值上的分布情况,这与分析量子态的原理略有不同,因为可能出现多个定态具有同一能量值,即出现所谓的简并能量态情况。
如果经典范畴中涉及的位移、动量之间的关系还远未达到不确定性原理所设定的极限,通常可以采用麦克斯韦-玻尔兹曼统计来代替费米–狄拉克统计,这样做可以简化数学计算的难度。如果粒子平均间距R{\displaystyle {\bar {R}}}rR 远大于粒子的平均物质波波长。{\displaystyle {\bar {\lambda }}}就可以采用上述经典范畴的处理方式。
灵遁者量子力学科普书籍《见微知著》在灵遁者淘宝有。
砖头|大楼|费米子|费米|狄拉克---傻大方小编总结的关键词

1926年,拉尔夫·福勒在描述恒星向白矮星的转变过程中,首次应用了费米–狄拉克统计的原理。由恒星演变而来的白矮星,是另一个不属于经典范畴、必须采用费米–狄拉克统计的例子。尽管白矮星的温度很高(其表面温度通常能达到10,000开尔文),但是它内部高度聚集的电子和每个电子的低质量,使得处理这问题必须采用费米–狄拉克统计,而不能用经典的波尔兹曼统计近似处理。
1927年,阿诺·索末菲将费米–狄拉克统计应用到他对于金属电子的研究中。对于常温(约300开尔文)下金属中的电子,由于R远小于物质波的波长{\displaystyle {\bar {R}}\approx {\bar {\lambda }}/25},因此该系统远离经典范畴。这是因为电子质量较小,并且在金属中聚集程度较高。这样,为了分析金属中的传导电子,必须采用费米–狄拉克统计。
砖头|大楼|费米子|费米|狄拉克---傻大方小编总结的关键词
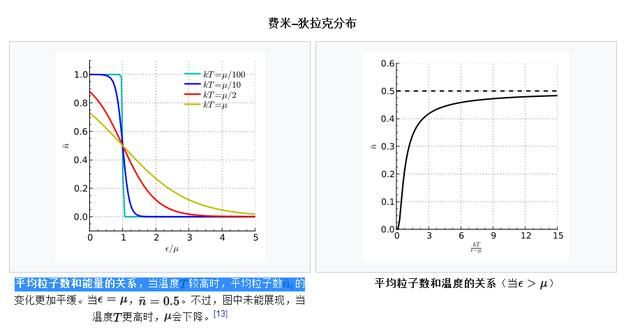
1928年,福勒和L·W·诺德汉在场致电子发射的研究中,也采用了这一统计规律。直至今日,费米–狄拉克统计仍然是物理学的一个重要部分。
在上一章中,我们提到了麦麦克斯韦-玻尔兹曼统计和玻色—爱因斯坦统计。那么这两个统计和现在讲的费米—狄拉克统计有什么不同和区别呢?
麦克斯韦-玻尔兹曼统计的粒子是可分辨的,它的应用还属于经典物理范围。比如气体,水分子运动。
费米-狄拉克统计的粒子是费米子,最常运用在电子统计方面。该统计要求每个能量状态只可能占据一个粒子。所以会构成“层级”。我们通常说费米子是构成物质的材料。玻色子是维持这些费米子的组成的中介。
砖头|大楼|费米子|费米|狄拉克---傻大方小编总结的关键词

波色-爱因斯坦统计粒子不可分别,但是每个状态可以被占据的粒子数没有限制。
这就是它们的不同和区别。我知道上面所有的内容,还是有太多专有名词,科普学习还是太难,公式更是会让大家一头雾水。
砖头|大楼|费米子|费米|狄拉克---傻大方小编总结的关键词

我再给大家举一个简单通俗的例子,来说明它们之间的不同和区别。就好像一座大楼。
你要描述这座大楼的整体性质,比如说温度性质。你就要考虑组成大楼物质所有成分的运动状态。这时候你要用麦克斯韦-玻尔兹曼统计来描述。就像你要描述水温,你要考虑水分子的运动情况,运动越剧烈,水温越高。
大楼的主要材料是砖头【费米子】,要描述砖头的运动和排列情况,就需要用费米—狄拉克统计。
而使得砖头【费米子】粘合的水泥沙子就可以看做是玻色子。所以玻色子可以出现在任何地方。同一能量级态容许多少玻色子存在。
砖头|大楼|费米子|费米|狄拉克---傻大方小编总结的关键词

这是我能想到的让大家好理解的通俗案例。比较粗俗,希望可以帮助大家理解。
这一章和上一章反复出现了不确定性原理。所以下一章会为大家介绍不确定性原理。
摘自独立学者,诗人,作家,国学起名师灵遁者量子力学科普书籍《见微知著》
- 【德媒聚焦】德国“大政府”还没正式组成,支持率却掉成了“少数
- Moncler开启人海战术 将启用八名设计师组成创意团队
- 江苏的两个县,以前归山东管 中原文化重要的组成部分
- 七家英国公司组成加密货币交易主体
- 昆明空气质量跌出全国前十!25名昆明市人大常委会组成人员提出质
- 节前慰问送温暖 扶贫帮困促发展
- 俄罗斯撮合,叙军与库尔德武装组成联军,决不让土耳其大军南下
- 大家记住:费米子是组成物质的粒子,玻色子是传递力的粒子!
- 多家钢铁企业去年业绩大幅提升,跨区域兼并重组成今年主基调
- 广西自治区政协原党组成员、副主席刘君因严重违纪被开除党籍
