领域|强化学习算法DeepCube，机器自行解决复杂魔方问题( 八 ) 自行解决|rl|强化|机器|算法

论文结果
论文的结果令人印象深刻。在使用三个GPU并行训练了44小时之后，网络学会了类似甚至超过人工复原魔方的方案。最终，将本文模型DeepCube已与先前介绍的两种求解方法进行了比较，分别是Kociemba two-staged solver 和Korf IDA*。
为验证本文方法的效率，论文使用640个随机打乱的魔方对不同方法分别进行测试，并设置最大求解步骤为1000步，最大求解时间为1小时，实现发现DeepCube和Kociemba方法均能在限制步骤和时间内复原魔方。具体而言，Kociemba求解速度非常快，其中值仅为一秒钟，但是由于依赖人工定义规则，其求解并不总是最短的。DeepCube方法花费了更多的时间，中值约为10分钟，但在55％的情况，该方法会比Kociemba得到更好的复原方案，即更少的步骤。从我个人的角度来看，55％虽然不足以说NN明显更好，但至少证明该方法还不错。下图（摘自论文）显示了所有求解方法的复原步数分布。可以看到，由于复原时间较长，在1000步魔方复原测试中没有比较Korf求解方法，但为了将DeepCube与Korf求解方法的性能进行比较，论文进一步设计了更容易的15步魔方复原测试集。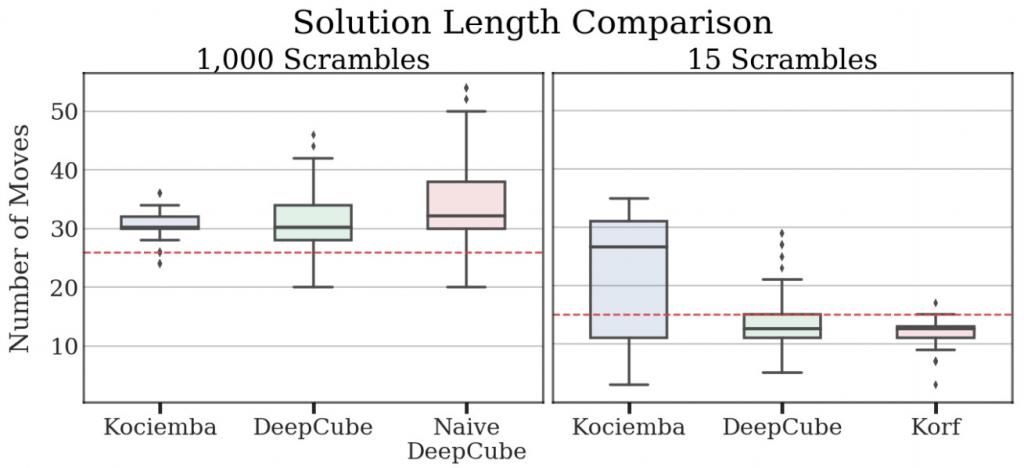

文章插图
实现细节
好的，现在我们开始介绍代码实现。在本部分中，我将简要介绍代码方案及一些关键设计，但在此之前，我还是要先强调一些事情：
我不是该项目的研究人员，因此这段代码只是想要复现论文的方法。但不幸的是，由于论文没有提供确切的超参数信息，因此我进行了大量猜测和试验，但实现结果与论文的结果依然存在较大差异。
同时，我试图以通用方式实施所有操作来简化实验。例如，有关魔方状态和转换的详细信息不做详细展示，仅仅通过添加一个新模块来抽象化3x3魔方问题。在我的代码中，分别对2x2魔方和3x3魔方进行实验，但类似这样有固定可预测动作集的、环境完全可见的问题都可以通过这样的方式进行解决。下一节会做详细说明。
相比代码性能，我更关注代码的可读性与简洁性，当然，对于不引入过多复杂性与成本消耗就能提高模型性能的操作，我在代码中还是保留了它们。例如，仅通过分割魔方数据集和正向网络传递，就可以将训练过程加快5倍。但是，如果需要将大多数内容重构为多GPU和多线程模式，我为简单起见就没有这样做。典型的就是MCTS进程，通常采用多线程代码实现，加快模型速度，但这就需要处理进程之间的同步问题。我没考虑那么多，只是以串行方式进行MCTS，仅对批量搜索进行了简单优化。
综上，我的代码由以下几部分组成：
魔方环境，用于定义观察/状态空间、可能的动作以及网络状态的表示，见libcube / cubes模块；